
【题目】如图,四棱锥P-ABCD中,底面![]() 为菱形,且
为菱形,且![]() ,
, ![]() .
.

(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题(1)取![]() 的中点
的中点![]() ,利用菱形和等边三角形的三线合一得到线线垂直,进而得到线面垂直和线线垂直;(2)先利用勾股定理和线面垂直的判定定理得到线面垂直,建立空间直角坐标系,利用空间向量进行求解.
,利用菱形和等边三角形的三线合一得到线线垂直,进而得到线面垂直和线线垂直;(2)先利用勾股定理和线面垂直的判定定理得到线面垂直,建立空间直角坐标系,利用空间向量进行求解.
试题解析:(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
∵![]() ,四边形
,四边形![]() 为菱形,且
为菱形,且![]() ,
,
∴![]() 和
和![]() 为两个全等的等边三角形,
为两个全等的等边三角形,
则![]()
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴![]() ;
;
(Ⅱ)解:在![]() 中,由已知得,
中,由已知得, ![]() ,
, ![]() ,
,
则![]() ,∴
,∴![]() ,
,
即![]() ,又
,又![]() ,∴
,∴![]() 平面
平面![]() ;
;
以点E为坐标原点,分别以EA,EB,EP所在直线为x,y,z轴,建立如图所示空间直角坐标系,
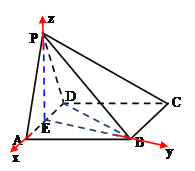
则E(0,0,0),C(-2, ![]() ,0),D(-1,0,0),P(0,0,
,0),D(-1,0,0),P(0,0, ![]() ),
),
则![]() =(1,0,
=(1,0, ![]() ),
),![]() =(-1,
=(-1, ![]() ,0),
,0),
由题意可设平面![]() 的一个法向量为
的一个法向量为![]() ;
;
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由已知得: 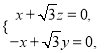 令y=1,则
令y=1,则![]() ,z=-1,
,z=-1,
∴![]() ;
;
则![]() ,所以
,所以![]()
![]()
![]() ,
,
由题意知二面角![]() 的平面角为钝角,
的平面角为钝角,
所以二面角![]() 的余弦值为
的余弦值为![]()


科目:高中数学 来源: 题型:
【题目】某城市的电视发射搭CD建在市郊的一座小山上,如图所示,小山高BC为30米,在地平面上有一点A,测得A,C两点间距离为50米.

(1)如果从点A观测电视发射塔的视角∠CAD=![]() ,求这座电视发射塔的高度;
,求这座电视发射塔的高度;
(2)点A在何位置时,角∠CAD最大.(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 与圆C相切,圆心C的坐标为
与圆C相切,圆心C的坐标为![]()
(1)求圆C的方程;
(2)设直线y=x+m与圆C交于M、N两点.
①若![]() ,求m的取值范围;
,求m的取值范围;
②若OM⊥ON,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年“十一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图的频率分布直方图.
,后得到如图的频率分布直方图.

(1)求这40辆小型车辆车速的众数和中位数的估计值;
(2)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆恰有一辆的概率.
的车辆恰有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感车天地关于某品牌汽车的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (千元)由如表的统计资料:
(千元)由如表的统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.1 | 3.4 | 5.9 | 6.6 | 7.0 |
(1)画出散点图并判断使用年限与所支出的维修费用是否线性相关;如果线性相关,求回归直线方程;
(2)若使用超过8年,维修费用超过1.5万元时,车主将处理掉该车,估计第10年年底时,车主是否会处理掉该车?
( )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 和
和![]() 是椭圆
是椭圆![]() 的两个焦点,且点
的两个焦点,且点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)直线![]() (m>0)与椭圆C有且仅有一个公共点,且与x轴和y轴分别交于点M,N,当△OMN面积取最小值时,求此时直线
(m>0)与椭圆C有且仅有一个公共点,且与x轴和y轴分别交于点M,N,当△OMN面积取最小值时,求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和
项和![]() ,对任意正整数
,对任意正整数![]() ,总存在正数
,总存在正数![]() 使得
使得![]() ,
, ![]() 恒成立:数列
恒成立:数列![]() 的前
的前![]() 项和
项和![]() ,且对任意正整数
,且对任意正整数![]() ,
, ![]() 恒成立.
恒成立.
(1)求常数![]() 的值;
的值;
(2)证明数列![]() 为等差数列;
为等差数列;
(3)若![]() ,记
,记![]()
![]() ,是否存在正整数
,是否存在正整数![]() ,使得对任意正整数
,使得对任意正整数![]() ,
, ![]() 恒成立,若存在,求正整数
恒成立,若存在,求正整数![]() 的最小值,若不存在,请说明理由.
的最小值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com