
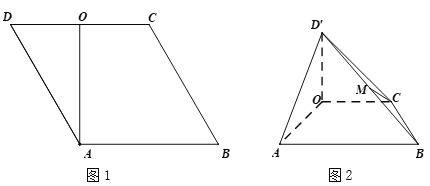
【题目】在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点(如图1).将
的中点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 的中点(如图2).
的中点(如图2).
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)当四棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
【答案】(Ⅰ)见解析. (Ⅱ)见解析. (Ⅲ) ![]() .
.
【解析】
(Ⅰ)证明OD'⊥AO. 推出OD'⊥平面ABCO. 然后证明OD'⊥BC.(Ⅱ)取P为线段AD'的中点,连接OP,PM;证明四边形OCMP为平行四边形,然后证明CM∥平面AOD';(Ⅲ)说明OD'是四棱锥D'﹣ABCO的高.通过体积公式求解即可.
(Ⅰ)证明:因为在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() .
.
因为平面![]() 平面
平面![]()
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
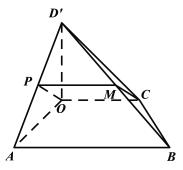
(Ⅱ)证明:如图,取![]() 为线段
为线段![]() 的中点,连接OP,PM;
的中点,连接OP,PM;
因为在![]() 中,
中,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,
的中点,
所以![]() ,
,![]() .
.
因为![]() 是线段
是线段![]() 的中点,菱形
的中点,菱形![]() 中,
中,![]() ,
,![]() ,
,
所以![]() .
.
所以![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(Ⅲ)由(Ⅰ)知![]() 平面
平面![]() .
.
所以![]() 是四棱锥
是四棱锥![]() 的高,又S=
的高,又S=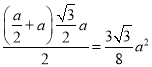 ,
,![]()
因为![]() ,
,
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,四边形ABCD是菱形,![]() ,BD=2.
,BD=2.
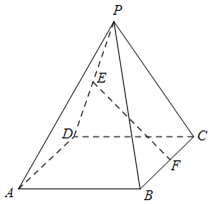
(1)若点E,F分别为线段PD,BC上的中点,求证:EF∥平面PAB;
(2)若平面PBD⊥平面ABCD,且PD⊥PB,PD=PB,求平面PAB与平面PBC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 在抛物线
在抛物线![]() :
: ![]() 上,直线
上,直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,且直线
两点,且直线![]() ,
, ![]() 的斜率之和为-1.
的斜率之和为-1.
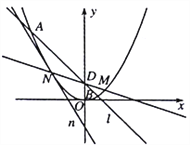
(1)求![]() 和
和![]() 的值;
的值;
(2)若![]() ,设直线
,设直线![]() 与
与![]() 轴交于
轴交于![]() 点,延长
点,延长![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,记直线
,记直线![]() ,
, ![]() 与
与![]() 轴围成的三角形面积为
轴围成的三角形面积为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形ABCD中,AB=1,AD![]() ,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
,且∠BAD=45°,以BD为折线,把△ABD折起,使AB⊥DC,连接AC,得到三棱锥A﹣BCD.
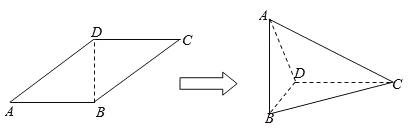
(1)求证:平面ABD⊥平面BCD;
(2)求二面角B﹣AC﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
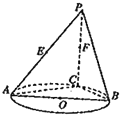
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知锐角△ABC中,角A,B,C的对边分别为a,b,c,b+c=10,a=![]() ,5bsinAcosC+5csinAcosB=3a.
,5bsinAcosC+5csinAcosB=3a.
(1)求A的余弦值;
(2)求b和c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3 000人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 | |||
调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 | y人 |
社会人士 | 500人 | x人 | z人 |
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.06.
(1)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,求这2人中恰好有1个人为在校学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD是边长为3的菱形,∠ABC=60°.PA⊥面ABCD,且PA=3.F在棱PA上,且AF=1,E在棱PD上.
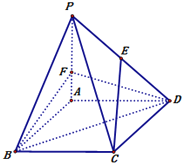
(Ⅰ)若CE∥面BDF,求PE:ED的值;
(Ⅱ)求二面角B-DF-A的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com