已知平面内的动点P到点F(1,0)的距离比到直线x=-2的距离小1.
(1)求点P的轨迹C的方程;
(2)若A、B为轨迹C上的两点,已知FA⊥FB,且△FAB的面积S△FAB=4,求直线AB的方程.
【答案】
分析:(1)设动点P的坐标为(x,y),根据动点P到点F(1,0)的距离比到直线x=-2的距离小1.代入两点之间距离公式,及点到直线的距离公式,化简即可得到点P的轨迹C的方程;
(2)设直线AB的方程为x=ty+m,结合FA⊥FB,且△FAB的面积S
△FAB=4,我们可以构造出关于m的方程,解方程求出m值,即可求出满足条件的直线AB的方程.
解答:(1)设点P(x,y),根据题意得
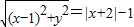
当
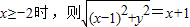
两边平方化简得y
2=4x
当x<-2时,则
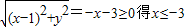
又由
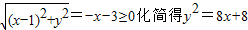
得x≥-1与x<-2矛盾
故点P的轨迹C的方程为y
2=4x.
(2)设直线AB的方程为x=ty+m
由
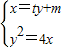
得y
2-4ty-4m=0
由△=16t
2+16m>0得t
2+m>0
设A(x
1,y
1),B(x
2,y
2)
则y
1+y
2=4t,y
1y
2=-4m
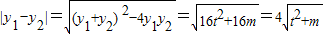
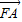
=(x
1-1,y
1),
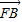
=(x
2-1,y
2)
由
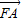
•
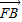
=0,得x
1•x
2-(x
1+x
2)+1+y
1•y
2=0
又由x
1=t•y
1+m,x
2=t•y
2+m,得4t
2=m
2-6m+1
S
△ABF=

|m-1|×4
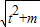
=|m-1|
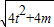
=|m-1|
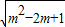
=(m-1)
2,
由(m-1)
2=4,解得m=-1,或m=3
将m=-1代入4t
2=m
2-6m+1得t
2=2,
将m=3代入4t
2=m
2-6m+1得4t
2=9-18+1=-8<O不成立,
∴m=3不合是题意舍去
∴所求直线AB的方程为x±
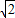
y+1=0
点评:本题考查的知识点是直线的一般式方程,抛物线的标准方程,直线与圆锥曲线的综合问题,(1)中关键是根据已知,构造关于动点P的方程,(2)的关键是“设而不求”+“联立方程”+“韦达定理”.

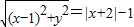
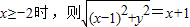
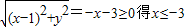
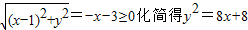
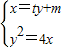 得y2-4ty-4m=0
得y2-4ty-4m=0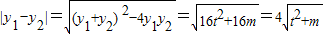
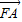 =(x1-1,y1),
=(x1-1,y1),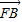 =(x2-1,y2)
=(x2-1,y2)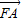 •
•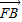 =0,得x1•x2-(x1+x2)+1+y1•y2=0
=0,得x1•x2-(x1+x2)+1+y1•y2=0 |m-1|×4
|m-1|×4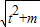 =|m-1|
=|m-1|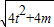 =|m-1|
=|m-1|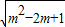 =(m-1)2,
=(m-1)2,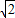 y+1=0
y+1=0

![]() .
.