
| A. | y=x2 | B. | y=x-2 | C. | $y={(\frac{1}{4})^{-|x|}}$ | D. | $y={log_3}{x^{\frac{5}{6}}}$ |
分析 根据函数奇偶性和单调性的性质进行判断即可.
解答 解:y=x2在区间(-∞,0)上是减函数,不满足条件.
y=x-2=$\frac{1}{{x}^{2}}$是偶函数,在(-∞,0)上是增函数,满足条件.
$y={(\frac{1}{4})^{-|x|}}$=4|x|,是偶函数,当x<0时,y=4-x=$(\frac{1}{4})$x为减函数,不满足条件.
$y={log_3}{x^{\frac{5}{6}}}$=log3$\root{6}{{x}^{5}}$,则函数的定义域为(0,+∞),定义域关于原点不对称,则函数f(x)为非奇非偶函数,不满足条件.
故选:B
点评 本题主要考查函数奇偶性和单调性的判断,要求熟练掌握常见函数的奇偶性和单调性的性质.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 4 | C. | -1或4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (-∞,0) | C. | (-1,0) | D. | [-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+i | B. | 1-i | C. | 2+i | D. | 2-i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
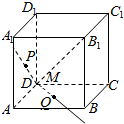 如图,M是正方体ABCD-A1B1C1D1对角线AC1上的动点,过点M作垂直于面ACC1A1的直线与正方体表面分别交于P、Q两点,设AM=x,PQ=y,则函数y=f(x)的图象大致为( )
如图,M是正方体ABCD-A1B1C1D1对角线AC1上的动点,过点M作垂直于面ACC1A1的直线与正方体表面分别交于P、Q两点,设AM=x,PQ=y,则函数y=f(x)的图象大致为( )| A. |  | B. | 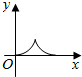 | C. | 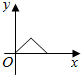 | D. | 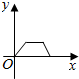 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
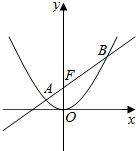 已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.
已知直线l经过抛物线x2=4y的焦点,且与抛物线交于A,B两点,点O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com