
【题目】在如图所示的几何体中,四边形![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 的中点,且
的中点,且![]() .
.
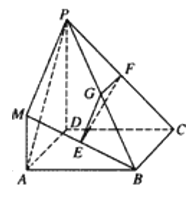
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:平面P![]() ;
;
科目:高中数学 来源: 题型:
【题目】设D是含数1的有限实数集,f(x)是定义在D上的函数。若f(x)的图像绕原点逆时针旋转![]() 后与原图像重合,则在以下各项中,f(1)的取值只可能是( )
后与原图像重合,则在以下各项中,f(1)的取值只可能是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 0
D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,D为边BC上一点,AD=6,BD=3, DC=2.
(1)若AD⊥BC,求∠BAC的大小;
(2)若∠ABC= ![]() ,求△ADC的面积.
,求△ADC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 数列{bn},{cn}满足 (n+1)bn=an+1﹣ ![]() ,(n+2)cn=
,(n+2)cn= ![]() ﹣
﹣ ![]() ,其中n∈N*.
,其中n∈N*.
(1)若数列{an}是公差为2的等差数列,求数列{cn}的通项公式;
(2)若存在实数λ,使得对一切n∈N*,有bn≤λ≤cn , 求证:数列{an}是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平顶山市公安局交警支队依据《中华人民共和国道路交通安全法》第![]() 条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以
条规定:所有主干道路凡机动车途经十字口或斑马线,无论转弯或者直行,遇有行人过马路,必须礼让行人,违反者将被处以![]() 元罚款,记
元罚款,记![]() 分的行政处罚.如表是本市一主干路段监控设备所抓拍的
分的行政处罚.如表是本市一主干路段监控设备所抓拍的![]() 个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
个月内,机动车驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
违章驾驶员人数 |
|
|
|
|
|
(Ⅰ)请利用所给数据求违章人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ)预测该路段![]() 月份的不“礼让斑马线”违章驾驶员人数.
月份的不“礼让斑马线”违章驾驶员人数.
参考公式: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某抛掷骰子游戏中,规定游戏者可以有三次机会抛掷一颗骰子,若游戏者在前两次抛掷中至少成功一次才可以进行第三次抛掷,其中抛掷骰子不成功得0分,第1次成功得3分,第2次成功得3分,第3次成功得4分.游戏规则如下:抛掷1枚骰子,第1次抛掷骰子向上的点数为奇数则记为成功,第2次抛掷骰子向上的点数为3的倍数则记为成功,第3次抛掷骰子向上的点数为6则记为成功.用随机变量![]() 表示该游戏者所得分数.
表示该游戏者所得分数.
(1)求该游戏者有机会抛掷第3次骰子的概率;
(2)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某运动员每次投篮命中的概率等于![]() .现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
.现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三个随机数为一组,代表三次投篮的结果.经随机模拟产生了如下20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,该运动员三次投篮恰有两次命中的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 将1至![]() 这
这![]() 个自然数随机填入n×n方格的
个自然数随机填入n×n方格的![]() 个方格中,每个方格恰填一个数(
个方格中,每个方格恰填一个数(![]() ).对于同行或同列的每一对数,都计算较大数与较小数的比值,在这
).对于同行或同列的每一对数,都计算较大数与较小数的比值,在这![]() 个比值中的最小值,称为这一填数法的“特征值”.
个比值中的最小值,称为这一填数法的“特征值”.
(1)若![]() ,请写出一种填数法,并计算此填数法的“特征值”;
,请写出一种填数法,并计算此填数法的“特征值”;
(2)当![]() 时,请写出一种填数法,使得此填数法的“特征值”为
时,请写出一种填数法,使得此填数法的“特征值”为![]() ;
;
(3)求证:对任意一个填数法,其“特征值”不大于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了![]() 名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为选手成绩“优秀”与文化程度有关?
的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
(2)若参赛选手共![]() 万人,用频率估计概率,试估计其中优秀等级的选手人数;
万人,用频率估计概率,试估计其中优秀等级的选手人数;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com