
【题目】某学校为了解全校学生的体重情况,从全校学生中随机抽取了100 人的体重数据,得到如下频率分布直方图,以样本的频率作为总体的概率.
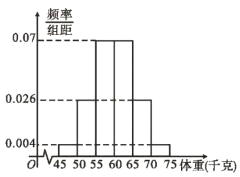
(1)估计这100人体重数据的平均值![]() 和样本方差
和样本方差![]() ;(结果取整数,同一组中的数据用该组区间的中点值作代表)
;(结果取整数,同一组中的数据用该组区间的中点值作代表)
(2)从全校学生中随机抽取3名学生,记![]() 为体重在
为体重在![]() 的人数,求
的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)由频率分布直方图可以认为,该校学生的体重![]() 近似服从正态分布
近似服从正态分布![]() .若
.若![]() ,则认为该校学生的体重是正常的.试判断该校学生的体重是否正常?并说明理由.
,则认为该校学生的体重是正常的.试判断该校学生的体重是否正常?并说明理由.
科目:高中数学 来源: 题型:
【题目】某公司为了鼓励运动提高所有用户的身体素质,特推出一款运动计步数的软件,所有用户都可以通过每天累计的步数瓜分红包,大大增加了用户走步的积极性,所以该软件深受广大用户的欢迎.该公司为了研究“日平均走步数和性别是否有关”,统计了2019年1月份所有用户的日平均步数,规定日平均步数不少于8000的为“运动达人”,步数在8000以下的为“非运动达人”,采用按性别分层抽样的方式抽取了100个用户,得到如下列联表:
运动达人 | 非运动达人 | 总计 | |
男 | 35 | 60 | |
女 | 26 | ||
总计 | 100 |
(1)(i)将![]() 列联表补充完整;
列联表补充完整;
(ii)据此列联表判断,能否有![]() 的把握认为“日平均走步数和性别是否有关”?
的把握认为“日平均走步数和性别是否有关”?
(2)从样本中的运动达人中抽取7人参加“幸运抽奖”活动,通过抽奖共产生2位幸运用户,求这2位幸运用户恰好男用户和女用户各一位的概率.
附:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是梯形.BC∥AD,AB=BC=CD=1,AD=2,![]() ,
,![]()
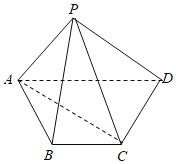
(Ⅰ)证明;AC⊥BP;
(Ⅱ)求直线AD与平面APC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁、网购、移动支付和共享单车被誉为中国的“新四大发明”,彰显出中国式创新的强劲活力.某移动支付公司从我市移动支付用户中随机抽取100名进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 10 | 8 | 7 | 3 | 2 | 15 |
女 | 5 | 4 | 6 | 4 | 6 | 30 |
合计 | 15 | 12 | 13 | 7 | 8 | 45 |
(Ⅰ)把每周使用移动支付超过3次的用户称为“移动支付活跃用户”,能否在犯错误概率不超过0.005的前提下,认为是否为“移动支付活跃用户”与性别有关?
(Ⅱ)把每周使用移动支付6次及6次以上的用户称为“移动支付达人”,视频率为概率,在我市所有“移动支付达人”中,随机抽取4名用户.
①求抽取的4名用户中,既有男“移动支付达人”又有女“移动支付达人”的概率;
②为了鼓励男性用户使用移动支付,对抽出的男“移动支付达人”每人奖励300元,记奖励总金额为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附公式及表如下:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com