在等差数列
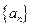
中,
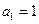
,前
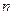
项和
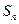
满足条件
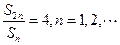
,
(1)求数列
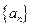
的通项公式和
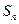
;
(2)记
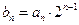
,求数列
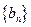
的前
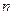
项和
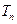
.
解:(1)设等差数列
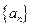
的公差为
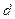
,由

得:
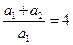
, (1分)
∴
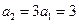
,(2分) 且
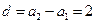
, (3分)
∴
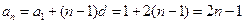
(4分)
∴
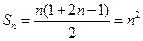
(5分)
(2)由
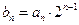
,得
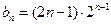
(6分) 所以
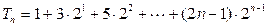
,……① (7分)
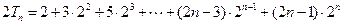
,……② (8分)
①-② 得
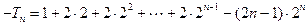
(9分)

(10分)
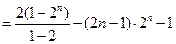
(11分
∴
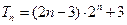
(12分)
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题14分)已知数列{
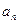
}的前
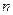
项和为
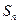
,且
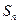
=
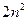
(
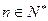
);
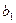
=3
且
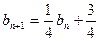
(
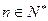
),
(1)写出
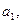
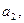
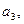
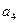
;
(2)求数列{
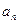
},{
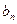
}的通项公式
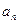
和
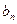
;
(3)设
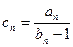
,求数列
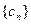
的前
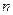
项和
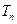
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)已知正数数列
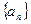
满足:
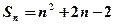
,其中
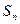
为数列
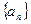
的前
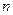
项和.
(1)求数列
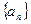
的通项
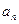
;
(2)令
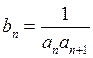
,求
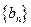
的前n项和
Tn..
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(13分)已知数列
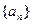
的前n项和为
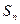
,并且满足
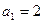
,
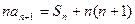
,
(1)求
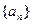
的通项公式;
(2)令
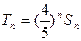
,问是否存在正整数
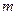
,对一切正整数
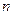
,总有
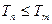
,若存在,求
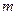
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
在数列
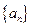
中,
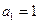
,
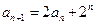
.
(1)设
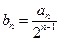
.证明:数列

是等差数列;
(2)求数列
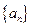
的前
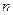
项和
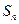
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
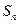
是公差不等于0的等差数列
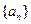
的前
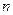

项和,若
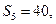
且
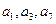
成等比
数列,则
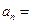
___。
查看答案和解析>>

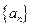 中,
中,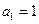 ,前
,前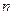 项和
项和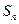 满足条件
满足条件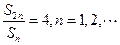 ,
,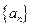 的通项公式和
的通项公式和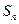 ;
;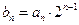 ,求数列
,求数列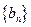 的前
的前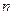 项和
项和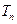 .
. 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案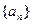 的前n项和为
的前n项和为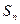 ,并且满足
,并且满足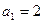 ,
,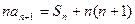 ,
,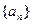 的通项公式;
的通项公式;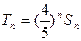 ,问是否存在正整数
,问是否存在正整数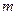 ,对一切正整数
,对一切正整数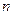 ,总有
,总有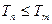 ,若存在,求
,若存在,求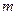 的值;若不存在,说明理由.
的值;若不存在,说明理由.