
分析 (1)设g(x)=ax(a>0且a≠1),由g(3)=8可确定y=g(x)的解析式,故y=$f(x)=\frac{{n-{2^x}}}{{m+{2^{x+1}}}}$,依题意,f(0)=0可求得n,从而可得y=f(x)的解析式;
(2)若h(x)=f(x)+a在(-1,1)上有零点,利用零点存在定理,由h(-1)h(1)<0,可求a的取值范围;
(3)由(2)知奇函数f(x)在R上为减函数,对任意的t∈(-4,4),不等式f(6t-3)+f(t2-k)<0恒成立?6t-3>k-t2,分离参数k,利用二次函数的单调性可求实数k的取值范围.
解答 (本小题12分)
(1)设g(x)=ax(a>0且a≠1),∵g(3)=8,∴a3=8,解得a=2.
∴g(x)=2x.…(1分)
∴$f(x)=\frac{{n-{2^x}}}{{m+{2^{x+1}}}}$,
∵函数f(x)是定义域为R的奇函数,∴f(0)=0,∴$\frac{n-1}{2+m}=0$=0,∴n=1,
∴$f(x)=\frac{{1-{2^x}}}{{m+{2^{x+1}}}}$又f(-1)=f(1),∴$\frac{{1-\frac{1}{2}}}{m+1}=-\frac{1-2}{4+m}$=,解得m=2
∴$f(x)=\frac{{1-{2^x}}}{{2+{2^{x+1}}}}$.…(3分)
(2)由(1)知$f(x)=\frac{{1-{2^x}}}{{2+{2^{x+1}}}}=-\frac{1}{2}+\frac{1}{{{2^x}+1}}$,
易知f(x)在R上为减函数,…(4分)
又h(x)=f(x)+a在(-1,1)上有零点,
从而h(-1)h(1)<0,即$({-\frac{1}{2}+\frac{1}{{\frac{1}{2}+1}}+a})({-\frac{1}{2}+\frac{1}{2+1}+a})<0$,…(6分)
∴(a+$\frac{1}{6}$)(a-$\frac{1}{6}$)<0,
∴-$\frac{1}{6}$<a<$\frac{1}{6}$,
∴a的取值范围为(-$\frac{1}{6}$,$\frac{1}{6}$);…(8分)
(3)由(1)知$f(x)=\frac{{1-{2^x}}}{{2+{2^{x+1}}}}=-\frac{1}{2}+\frac{1}{{{2^x}+1}}$,
又f(x)是奇函数,∴f(6t-3)+f(t2-k)<0,
∴f(6t-3)<-f(t2-k)=f(k-t2),
∵f(x)在R上为减函数,由上式得6t-3>k-t2,…(10分)
即对一切t∈(-4,4),有t2+6t-3>k恒成立,
令m(t)=t2+6t-3,t∈(-4,4),易知m(t)>-12,…(11分)
∴k<-12,即实数k的取值范围是(-∞,-12).…(12分)
点评 本题考查函数恒成立问题,考查函数奇偶性与单调性的应用,考查零点存在定理及二次函数的性质,考查函数方程思想、转化思想与运算求解能力,属于综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
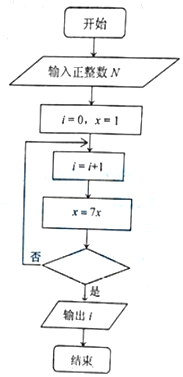 某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )| A. | x≤N | B. | x<N | C. | x>N | D. | x≥N |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{5}$] | B. | [-$\frac{1}{5}$,1] | C. | (-$\frac{1}{5}$,$\frac{1}{3}$] | D. | ($\frac{1}{3}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y<xz | B. | x<z<y | C. | z<y<x | D. | x<y<z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2${\;}^{(1-kt)(x-b)^{2}}$,(其中,t为关税的税率,且t∈[0,$\frac{1}{2}$),x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时的市场供应量曲线如图.
据调查分析,若干年内某产品关税与市场供应量P的关系近似地满足:y=P(x)=2${\;}^{(1-kt)(x-b)^{2}}$,(其中,t为关税的税率,且t∈[0,$\frac{1}{2}$),x为市场价格,b,k为正常数),当t=$\frac{1}{8}$时的市场供应量曲线如图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| ξ | -1 | 0 | 1 | 2 |
| P | x | $\frac{1}{3}$ | $\frac{1}{6}$ | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com