
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
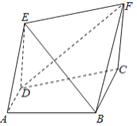
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]() .
.
【解析】
(1)证明:![]() 四边形
四边形![]() 为矩形,
为矩形,![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
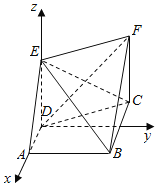
取![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
如图,则![]() ,0,
,0,![]() ,
,![]() ,2,
,2,![]() ,
,![]() ,2,
,2,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,2,
,2,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,2,
,2,![]() ,
,
由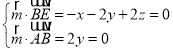 ,取
,取![]() ,得
,得![]() ,0,
,0,![]() ,
,
又![]() ,2,
,2,![]() ,
,![]()
![]() ,
,![]()
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)![]() ,0,
,0,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,2,
,2,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
则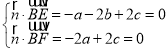 ,取
,取![]() ,得
,得![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
则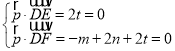 ,取
,取![]() ,得
,得![]() ,1,
,1,![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则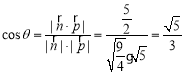 ,
,
![]() 二面角
二面角![]() 的正弦值
的正弦值![]() .
.
(3)假设在线段![]() 上存在点
上存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,
,
![]()
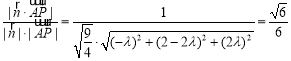 ,
,
解得![]() 或
或![]() ,
,
![]() ,
,![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知定点F(1,0),点A在x轴的非正半轴上运动,点B在y轴上运动,满足![]() 0,A关于点B的对称点为M,设点M的轨迹为曲线C.
0,A关于点B的对称点为M,设点M的轨迹为曲线C.
(1)求C的方程;
(2)已知点G(3,﹣2),动直线x=t(t>3)与C相交于P,Q两点,求过G,P,Q三点的圆在直线y=﹣2上截得的弦长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆规是用来画椭圆的一种器械,它的构造如图所示,在一个十字形的金属板上有两条互相垂直的导槽,在直尺上有两个固定的滑块A,B,它们可分别在纵槽和横槽中滑动,在直尺上的点M处用套管装上铅笔,使直尺转动一周,则点M的轨迹C是一个椭圆,其中|MA|=2,|MB|=1,如图,以两条导槽的交点为原点O,横槽所在直线为x轴,建立直角坐标系.
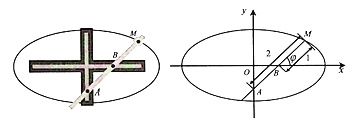
(1)将以射线Bx为始边,射线BM为终边的角xBM记为φ(0≤φ<2π),用![]() 表示点M的坐标,并求出C的普通方程;
表示点M的坐标,并求出C的普通方程;
(2)已知过C的左焦点F,且倾斜角为α(0≤α![]() )的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当
)的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当![]() ,|GH|,
,|GH|,![]() 依次成等差数列时,求直线l2的普通方程.
依次成等差数列时,求直线l2的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过定点
,过定点![]() 的直线l与椭圆E相交于A,B两点,C为椭圆的左顶点,当直线l过点
的直线l与椭圆E相交于A,B两点,C为椭圆的左顶点,当直线l过点![]() 时,
时,![]() (O为坐标原点)的面积为
(O为坐标原点)的面积为![]() .
.
(1)求椭圆E的方程;
(2)求证:当直线l不过C点时,![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定数列![]() .对
.对![]() ,该数列前
,该数列前![]() 项
项![]() 的最小值记为
的最小值记为![]() ,后
,后![]() 项
项![]() 的最大值记为
的最大值记为![]() ,令
,令![]() .
.
(1)设数列![]() 为2,1,6,3,写出
为2,1,6,3,写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)设![]() 是等比数列,公比
是等比数列,公比![]() ,且
,且![]() ,证明:
,证明:![]() 是等比数列;
是等比数列;
(3)设![]() 是公差大于0的等差数列,且
是公差大于0的等差数列,且![]() ,证明:
,证明:![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)+B的部分图象如图所示,其中A>0,ω>0,|φ|![]() .
.
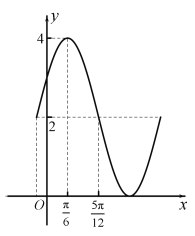
(Ⅰ)求函数y=f(x)解析式;
(Ⅱ)求x∈[0,![]() ]时,函数y=f(x)的值域.
]时,函数y=f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥D-ABC中![]() 为锐角三角形,平面ACD⊥平面
为锐角三角形,平面ACD⊥平面![]() .
.
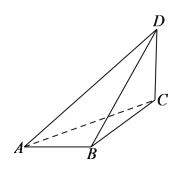
(1)求证:CD⊥平面ABC
(2)若直线BD与平面ACD所成角的正弦值为![]() ,求二面角D-AB-C的余弦值.
,求二面角D-AB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“挑战不可能”的电视节目上,甲、乙、丙三个人组成的解密团队参加一项解密挑战活动,规则是由密码专家给出题目,然后由![]() 个人依次出场解密,每人限定时间是
个人依次出场解密,每人限定时间是![]() 分钟内,否则派下一个人.
分钟内,否则派下一个人.![]() 个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲
个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲![]() 次的测试记录,绘制了如下的频率分布直方图.
次的测试记录,绘制了如下的频率分布直方图.
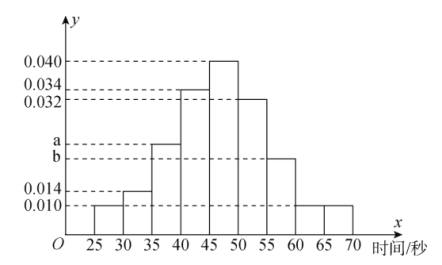
(1)若甲解密成功所需时间的中位数为![]() ,求
,求![]() 、
、![]() 的值,并求出甲在
的值,并求出甲在![]() 分钟内解密成功的频率;
分钟内解密成功的频率;
(2)在“挑战不可能”节目上由于来自各方及自身的心理压力,甲,乙,丙解密成功的概率分别为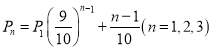 ,其中
,其中![]() 表示第
表示第![]() 个出场选手解密成功的概率,并且
个出场选手解密成功的概率,并且![]() 定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
①求该团队挑战成功的概率;
②该团队以![]() 从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目
从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
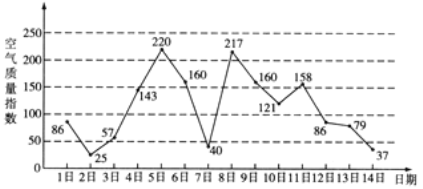
(1)求此人到达当日空气重度污染的概率;
(2)求此人在该市停留期间只有1天空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com