
分析 由已知得a1=1,$\frac{{a}_{n}}{{a}_{n-1}}=\frac{n-1}{n}$,n≥2,由此利用累乘法能求出数列{an}的通项公式.
解答 解:∵数列{an}满足a1=1,nan=(n-1)an-1(n≥2),
∴$\frac{{a}_{n}}{{a}_{n-1}}=\frac{n-1}{n}$,n≥2,
∴${a}_{n}={a}_{1}×\frac{{a}_{2}}{{a}_{1}}×\frac{{a}_{3}}{{a}_{2}}×…×\frac{{a}_{n}}{{a}_{n-1}}$
=1×$\frac{1}{2}×\frac{2}{3}×\frac{3}{4}$×…×$\frac{n-1}{n}$=$\frac{1}{n}$.
故数列{an}的通项公式为an=$\frac{1}{n}$.
点评 本题考查数列的通项公式的求法,是基础题,解题时要注意累乘法的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
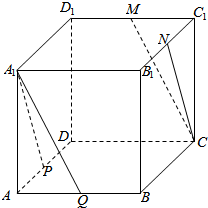 在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:
在正方体ABCD-A1B1C1D1中,P,Q,M,N分别为AD,AB,C1D1,B1C1的中点,求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com