
����Ŀ��ij�ִ���˾�����200��Ԫ����һ���ִ�����ÿ��40��Ԫ�ļ۸��������˹�˾.�ִ���˾�����ִ���ά������һ��ά����Ϊ4��Ԫ�������ִ���ʹ����ĥ���Ժ�ÿ���ά���ѱ���һ���2��Ԫ��ͬʱ���ִ���![]() ��ĩ������
��ĩ������![]() ��Ԫ�ļ۸����.
��Ԫ�ļ۸����.
��1��д���ִ���˾����![]() ��ĩ����������
��ĩ����������![]() ��Ԫ����
��Ԫ����![]() �ĺ�������ʽ������
�ĺ�������ʽ������![]() �����ֵ��
�����ֵ��
��2��Ϊʹ�ִ���˾��ƽ����������ִ���˾Ӧ�ڵڼ���ĩ�����ִ���
���𰸡�(1) ![]()
![]() ��191��Ԫ (2) ��7��ĩ
��191��Ԫ (2) ��7��ĩ
��������
��1������������������ȥ��֧����������������ά���Ѻ������룬���ɵõ���������ʽ�����ɶ��κ��������ʼ�![]() ��ȡֵ��Χ���ɵ����ֵ��
��ȡֵ��Χ���ɵ����ֵ��
��2�����ִ���˾��ƽ������Ϊ![]() ����Ԫ������
����Ԫ������![]() �����û�������ʽ������ֵ.
�����û�������ʽ������ֵ.
�⣺��1���ִ���˾![]() �����ά����Ϊ
�����ά����Ϊ![]() ��
��
������Ϊ![]()
�����ִ���˾����![]() ��ĩ����������
��ĩ����������![]()
![]() ��
��
![]()
��Ϊ![]() ������
������![]() ����Ԫ��.
����Ԫ��.
��2�����ִ���˾��ƽ������Ϊ![]() ����Ԫ������
����Ԫ������![]() .
.
��Ϊ![]() �����ҽ���
�����ҽ���![]() ʱ���Ⱥų�����������
ʱ���Ⱥų�����������![]() .
.
��Ϊʹ�ִ���˾��ƽ����������ִ���˾Ӧ�ڵ�7��ĩ�����ִ�.


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����幺����Ʊ��Ʊ�����±���
��Ʊ���� | 1~50 | 51~100 | 100���� |
��Ʊ�۸� | 13Ԫ/�� | 11Ԫ/�� | 9Ԫ/�� |
��ij��λҪ��֯���г�������������Ա�������ù�������������Ϊ���壬ѡ��������ͬ��ʱ��ֱ�Ʊ������������֧����Ʊ��Ϊ1290Ԫ�����������ź���һ����Ϊһ�����壬ͬһʱ�乺Ʊ������������֧����Ʊ��Ϊ990Ԫ����ô���������ŵ�����֮��Ϊ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABC�У�PA��AB��PA��BC��AB��BC��PA��AB��BC��2��DΪ�߶�AC���е㣬EΪ�߶�PC��һ��.

(1)��֤��PA��BD��
(2)��֤��ƽ��BDE��ƽ��PAC��
(3)��PA��ƽ��BDEʱ��������E��BCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ���������
���������![]() ��
��![]() �������߷��̣�
�������߷��̣�
��2����![]() ����ֻ�����������⣬��
����ֻ�����������⣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���еĹ�����˾Ϊ�˷���������У���ѧ�滮����Ͷ�ţ���һ����Ա�ܼ������ض�����һ�����վ��Ϊ���о������������ʱ��![]() ��˿͵Ⱥ�����
��˿͵Ⱥ�����![]() ֮��Ĺ�ϵ����������õ��������ݣ�
֮��Ĺ�ϵ����������õ��������ݣ�
���ʱ�䣨 | 10 | 11 | 12 | 13 | 14 | 15 |
�Ⱥ������� | 23 | 25 | 26 | 29 | 28 | 31 |
����С���ȴ���6��������ѡȡ4�����������Իع鷽�̣�����ʣ�µ�2�����ݽ��м���.���鷽�����£�������õ����Իع鷽�̼�����ʱ���Ӧ�ĵȺ�����![]() ������
������![]() ��ʵ�ʵȺ�����
��ʵ�ʵȺ�����![]() �IJ����ֵ�ľ���ֵ������1�������������ǡ���ع鷽����.
�IJ����ֵ�ľ���ֵ������1�������������ǡ���ع鷽����.
��1����ѡȡ���Ǻ���4�����ݣ���![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
��2���жϣ�1���еķ����Ƿ�����ǡ���ع鷽������
��3��Ϊ��ʹ�Ⱥ�ij˿Ͳ�����35�ˣ����ã�1���з��̹��Ƽ��ʱ������������Ϊ���٣���ȷ�����������ӣ�
��������һ������![]() ��
��![]() ������
������![]() ����ع�ֱ��
����ع�ֱ��![]() ��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��
��б�ʺͽؾ����С���˹��Ʒֱ�Ϊ��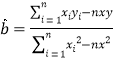
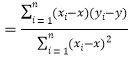 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У��ı���
�У��ı���![]() Ϊ���Σ���
������![]() ��
��![]() ��
��![]() �ֱ�Ϊ��
�ֱ�Ϊ��![]() ��
��![]() ���е㣮
���е㣮

��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ƽ��
ƽ��![]() ��
��![]() ����ƽ��
����ƽ��![]() ��ƽ��
��ƽ��![]() ���ɶ���ǵ�����ֵ��
���ɶ���ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017�ꡰʮһ���ڼ䣬���ٹ�·�����϶࣮ij���鹫˾��һ����������������С�������а������������Ⱥ�ÿ���50���ͳ�ȡһ���ij���������ȡ40����ʻԱ����ѯ�ʵ��飬��������ij�θ��ٹ�·�ij��٣�![]() ���ֳ����Σ�
���ֳ����Σ� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ����õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��
����õ���ͼ��Ƶ�ʷֲ�ֱ��ͼ��

��1������40��С�ͳ������ٵ���������λ���Ĺ���ֵ��
��2�����ӳ�����![]() �ij������γ�ȡ2����������
�ij������γ�ȡ2����������![]() �ij���ǡ��һ���ĸ��ʣ�
�ij���ǡ��һ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����ABCD�DZ߳�Ϊ1�������Σ�PA�͵���ABCD��PA��1����M����PC�ϵ�һ�㣬��AM��PB��
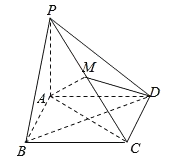
��1��������C��PBD�������
��2��֤����AM��ƽ��PBD��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com