
定义在R上函数y=f(x)是减函数,且函数y=f(x-1)的图像关于(1,0)成中心对称,若s,t满足不等式f(s2-2s)≤-f(2t-t2),则当1≤s≤4时, 的取值范围是( )
的取值范围是( )
A.  | B. | C.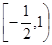 | D. |
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:单选题
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的容积为 立方米,且
立方米,且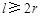 . 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )
. 假设该容器的建造费用仅与其表面积有关. 已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为22千元. 设该容器的建造费用为y千元. 当该容器建造费用最小时,r的值为( )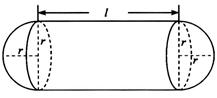
A. | B.1 | C.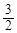 | D.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,B城市处于危险区内的时间为( )
| A.0.5小时 | B.1小时 | C.1.5小时 | D.2小时 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
(2014·大连模拟)已知f(x)=alnx+ x2,若对任意两个不等的正实数x1,x2都有
x2,若对任意两个不等的正实数x1,x2都有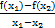 >0成立,则实数a的取值范围是( )
>0成立,则实数a的取值范围是( )
| A.[0,+∞) | B.(0,+∞) |
| C.(0,1) | D.(0,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com