【题目】如图所示，正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E、F且EF=
，则下列结论中错误的是（ ）
A.AC⊥BEB.EF
平面ABCD
C.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案科目：高中数学 来源： 题型：
【题目】如图是正方体的平面展开图，在这个正方体中，正确的命题是（ ）
A. BD与CF成60°角 B. BD与EF成60°角 C. AB与CD成60°角 D. AB与EF成60°角
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图给出的是2000年至2016年我国实际利用外资情况，以下结论正确的是（ ）
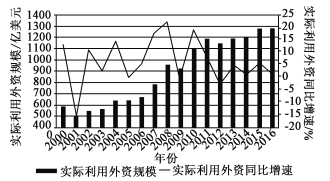
A. 2000年以来我国实际利用外资规模与年份呈负相关
B. 2010年以来我国实际利用外资规模逐年增大
C. 2008年以来我国实际利用外资同比增速最大
D. 2010年以来我国实际利用外资同比增速最大
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
（1）求抛物线方程;
（2）直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了支援湖北省应对新冠肺炎，某运输公司现有5名男司机，4名女司机，需选派5人运输一批紧急医用物资到武汉.
（1）如果派3名男司机、2名女司机，共有多少种不同的选派方法？
（2）至少有两名男司机，共有多少种不同的选派方法？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下图是我国2010年至2016年生活垃圾无害化处理量（单位：亿吨）的折线图
注：年份代码1~7分别对应年份2010~2016
（1）由折线图看出，可用线性回归模型拟合y与t的关系，请求出相关系数r，并用相关系数的大小说明y与t相关性的强弱；
（2）建立y关于t的回归方程（系数精确到0.01），预测2018年我国生活垃圾无害化处理量.
附注：
参考数据：
，
，
， 
.
参考公式：
相关系数
回归方程
中斜率和截距的最小二乘估计公式分别为：
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知平面直角坐标系xOy，在x轴的正半轴上，依次取点
，
，
，
，并在第一象限内的抛物线
上依次取点
，
，
，
，
，使得
都为等边三角形，其中
为坐标原点，设第n个三角形的边长为
．
⑴求
，
，并猜想
不要求证明)；
⑵令
，记
为数列
中落在区间
内的项的个数，设数列
的前m项和为
，试问是否存在实数
，使得
对任意
恒成立？若存在，求出的取值范围；若不存在，说明理由；
⑶已知数列
满足：
，数列
满足：
，求证：
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
