
【题目】如图,在四棱台ABCD﹣A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1. 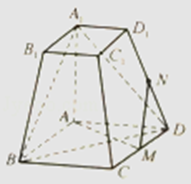
(1)求证:AM⊥A1B;
(2)若M为CD的中点,N为棱DD1上的点,且MN与平面A1BD所成角的正弦值为 ![]() ,试求DN的长.
,试求DN的长.
【答案】
(1)证明:在平行四边形ABCD中,∠BAD=120°,∴∠ADM=60°,
在△ADM中,AD=2,DM=1,∴ ![]() =
= ![]() ,
,
可得AD2=AM2+DM2,∴AM⊥CD.
又CD∥AB,∴AM⊥AB,
∵∠A1AB=∠A1AD=90°,∴A1A⊥AB,A1A⊥AD.
又∵AB∩AD=A,AB,AD平面ABCD,
∴AA1⊥ABCD,又AM平面ABCD,
∴AM⊥AA1.又∵AB∩AA1=A,AB,AA1平面AA1B1B,
∴AM⊥平面AA1B1B.又∵A1B平面AA1B1B,
∴AM⊥A1B
(2)解:∵M为CD的中点,DM=1,∴CD=2,
所以四边形ABCD为菱形.
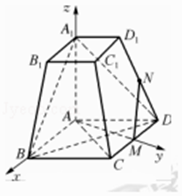
分别以AB,AM,AA1为x轴,y轴,z轴,建立如图所示的空间直角坐标系A﹣xyz,
则点 ![]() .
.
∴ ![]() .
.
设平面A1BD的一个法向量为 ![]() ,则有
,则有 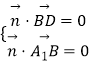 ,
,
∴ ![]() ,令x=1,则
,令x=1,则 ![]() ,
,
设 ![]() ,∴
,∴ ![]() ,
,
∴  ,
,
∴ ![]() ,∴2λ2﹣13λ+6=0,
,∴2λ2﹣13λ+6=0,
∴ ![]() 或λ=6(舍去).
或λ=6(舍去).
∴ ![]() .
.
【解析】(1)利用勾股定理逆定理得出AM⊥CD,即AM⊥AB,结合AM⊥AA1得出AM⊥平面AA1B1B,于是AM⊥A1B;(2)建立空间坐标系,根据MN与平面A1BD所成角的大小确定N点位置,从而得出DN的长.
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点,需要掌握垂直于同一个平面的两条直线平行才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】曲线C:ρ2﹣2ρcosθ﹣8=0 曲线E: ![]() (t是参数)
(t是参数)
(1)求曲线C的普通方程,并指出它是什么曲线.
(2)当k变化时指出曲线K是什么曲线以及它恒过的定点并求曲线E截曲线C所得弦长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象与函数h(x)=x+![]() +2的图象关于点A(0,1)对称.
+2的图象关于点A(0,1)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)+![]() ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个偶数组成的数阵排列如下:
2 4 8 14 22 32 …
6 10 16 24 34 … …
12 18 26 36 … … …
20 28 38 … … … …
30 40 … … … … …
42 … … … … … …
… … … … … … …
则第20行第4列的数为( )
A. 546 B. 540 C. 592 D. 598
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 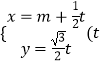 为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,椭圆C的极坐标方程为
为参数),以坐标原点为极点,以x轴正半轴为极轴建立极坐标系,椭圆C的极坐标方程为 ![]() ,且直线l经过椭圆C的右焦点F.
,且直线l经过椭圆C的右焦点F.
(1)求椭圆C的内接矩形PMNQ面积的最大值;
(2)若直线l与椭圆C交于A,B两点,求|FA||FB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量![]() (单位:千套)与销售价格
(单位:千套)与销售价格![]() (单位:元/套)满足的关系式
(单位:元/套)满足的关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求![]() 的值;
的值;
(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格![]() 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)

(Ⅰ)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(Ⅱ)经过多次测试后,甲每次解答一道几何题所用的时间在5—7分钟,乙每次解答一道几何题所用的时间在6—8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com