练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知△ABC中，a=1，b=3，∠C=60°，则S△ABC=$\frac{3\sqrt{3}}{4}$．

    分析 根据题意，由正弦定理可得S△ABC=$\frac{1}{2}$absinC，代入数据计算即可得答案．

    解答 解：根据题意，△ABC中，a=1，b=3，∠C=60°，
    则S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}$×1×3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$；
    故答案为：$\frac{3\sqrt{3}}{4}$．

    点评 本题考查三角形面积的计算，涉及正弦定理的运用，考查了计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

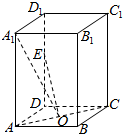    13．如图所示，在长方体体ABCD-A1B1C1D1中，O为AC的中点．
    （1）化简：$\overrightarrow{{A}_{1}O}$-$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{1}{2}$$\overrightarrow{AD}$；
    （2）设E是棱DD1上的点，且$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{D{D}_{1}}$，若$\overrightarrow{EO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$，试求实数x，y，z的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知某种物经过1000年衰减后，含量变为原来的80%，问多少年后该物质含量为原来的一半？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

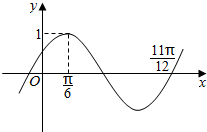    11．函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图示，将y=f（x）的图象向右平移$\frac{π}{6}$个单位后得到函数y=g（x）的图象，则g（x）的单凋递增区间为（　　）
    A．[2kπ-$\frac{π}{6}$，2kπ$+\frac{π}{3}$]B．[2k$π+\frac{π}{3}$，2kπ$+\frac{5π}{6}$]C．[kπ$+\frac{π}{3}$，kπ$+\frac{5π}{6}$]D．[kπ$-\frac{π}{6}$，kπ$+\frac{π}{3}$]，

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．若圆x2+y2+2x+2y+1=0的面积被直线ax+by+1=0（a＞0，b＞0）平分．则ab的最大值是（　　）
    A．$\frac{1}{16}$B．$\frac{1}{4}$C．4D．16

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知等差数列{an}的通项公式为an=3-2n，
    求：（1）-37是这个数列的第几项？（2）前10项和S10．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．设函数f（x）在点x0可导，且$\underset{lim}{h→0}$$\frac{f（{x}_{0}）-f（{x}_{0}-2h）}{h}$=3，则f′（x0）=（　　）
    A．$\frac{3}{2}$B．$\frac{2}{3}$C．-$\frac{3}{2}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．如图，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/时的速度前进，舰艇乙沿北偏东50°的方向以80海里/时的速度前进，1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E、F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

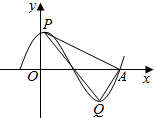    13．函数y=$\sqrt{3}$sin（ωx+φ）（ω＞0，φ＞0）的部分图象如图所示，设P，Q分别是图象的相邻的最高点和最低点，A是图象与x轴的交点，若AP⊥AQ，则ω的值为（　　）
    A．πB．$\frac{π}{2}$C．$\frac{π}{3}$D．$\frac{π}{4}$

    查看答案和解析>>

    同步练习册答案