
【题目】已知点(2,5)和(8,3)是函数y=﹣k|x﹣a|+b与y=k|x﹣c|+d的图象仅有的两个交点,那么a+b+c+d的值为
【答案】18
【解析】解:∵函数y=﹣k|x﹣a|+b与y=k|x﹣c|+d的图象交于两点(2,5),(8,3),
∴5=﹣k|2﹣a|+b ①
3=﹣k|8﹣a|+b ②
5=k|2﹣c|+d ③
3=k|8﹣c|+d ④
①﹣②得2=﹣k|2﹣a|+k|8﹣a|⑤
③﹣④得2=k|2﹣c|﹣k|8﹣c|⑥
⑤=⑥得|8﹣a|+|8﹣c|=|2﹣c|+|2﹣a|
即|8﹣a|﹣|2﹣a|+|8﹣c|﹣|2﹣c|=0
设f(x)=|8﹣x|﹣|2﹣x|,则f(a)+f(c)=0,
画出函数f(x)的图象,如图,其关于点A(5,0)成中心对称,
故点a与点c关于点A(5,0)成中心对称,
∴![]() (a+c)=5,
(a+c)=5,
∴a+c=10,
又∵函数y=﹣k|x﹣a|+b的对称轴为x=a,函数y=k|x﹣c|+d的对称轴为x=c,
∴2<a<8,2<c<8
②+③:8=﹣k(8﹣a)+b+k(c﹣2)+d,
∴b+d=8,
∴a+b+c+d=18
故答案为:18.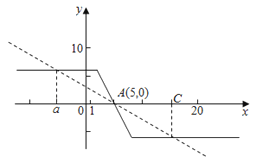
将两个交点代入函数y=﹣k|x﹣a|+b方程,得到方程组,将两个方程相减;据绝对值的意义及k的范围得到k,a满足的等式;同样的过程得到k,c满足的等式,两式联立求出a+c的值,再求出b+d,即可得到结论.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[50,60)的学生人数为6.
(Ⅰ)求直方图中x的值;
(Ⅱ)试估计所抽取的数学成绩的平均数;
(Ⅲ)试根据样本估计“该校高一学生期末数学考试成绩≥70”的概率.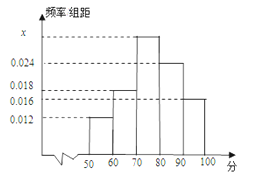
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场一年购进某种货物900吨,每次都购进x吨,运费为每次9万元,一年的总存储费用为9x万元.
(1)要使一年的总运费与总存储费用之和最小,则每次购买多少吨?
(2)要使一年的总运费与总存储费用之和不超过585万元,则每次购买量在什么范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P,Q是两个集合,定义集合P﹣Q={x|x∈P且xQ}为P,Q的“差集”,已知P={x|1﹣ ![]() <0},Q={x||x﹣2|<1},那么P﹣Q等于( )
<0},Q={x||x﹣2|<1},那么P﹣Q等于( )
A.{x|0<x<1}
B.{x|0<x≤1}
C.{x|1≤x<2}
D.{x|2≤x<3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司一年经销某种商品,年销售量400吨,每吨进价5万元,每吨销售价8万元.全年进货若干次,每次都购买x吨,运费为每次2万元,一年的总存储费用为2x万元.
(1)求该公司经销这种商品一年的总利润y与x的函数关系;
(2)要使一年的总利润最大,则每次购买量为多少?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2﹣4y﹣4=0,双曲线的左、右顶
点A、B是该圆与x轴的交点,双曲线与半圆相交于与x轴平行的直径的两端点.
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为F1、F2 , 试在“8”字形曲线上求点P,使得
∠F1PF2是直角.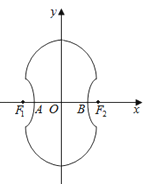
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]()
(1)求![]() 的值;
的值;
(2)当x∈(﹣t,t](其中t∈(﹣1,1),且t为常数)时,f(x)是否存在最小值,如果存在求出最小值;如果不存在,请说明理由;
(3)当f(x﹣2)+f(4﹣3x)≥0时,求满足不等式f(x﹣2)+f(4﹣3x)≥0的x的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线过点P(﹣3![]() , 4),它的渐近线方程为y=±
, 4),它的渐近线方程为y=±![]() x.
x.
(1)求双曲线的标准方程;
(2)设F1和F2为该双曲线的左、右焦点,点P在此双曲线上,且|PF1||PF2|=41,求∠F1PF2的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com