练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    (1)已知f(x-3)=x2+3x+1,求f(x)的解析式;

    (2)已知f(x)满足f(x-)=x2+,求函数f(x)的解析式;

    (3)已知函数f(x)是一次函数,且f［f(x)］=4x+1,求函数f(x)的解析式.

    思路解析:解决此类问题的关键是找出对应关系,找对应关系常用的方法有三种,即拼凑法、换元法、待定系数法.

    解:(1)方法一:拼凑法.

    ∵f(x-3)=x2+3x+1=(x-3)2+6x-9+3x+1=(x-3)2+9x-8=(x-3)2+9(x-3)+27-8

    =(x-3)2+9(x-3)+19,

    ∴f(x)=x2+9x+19.

    方法二:换元法.

    令t=x-3,则x=t+3,

    ∴f(t)=(t+3)2+3(t+3)+1=t2+9t+19.

    ∴f(x)=x2+9x+19.

    (2)设x-=t,则(x-)2=t2,∴x2+=t2+2.∴f(t)=t2+2.

    ∴所求函数的解析式为f(x)=x2+2.

    (3)设f(x)=kx+b(k≠0),

    ∴f［f(x)］=f(kx+b)=k(kx+b)+b=k2x+kb+b.

    又∵对x∈R总有f［f(x)］=k2x+kb+b=4x+1,

    ∴

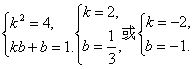
    ∴f(x)的解析式为f(x)=2x+,或f(x)=-2x-1.

    深化升华

    (1)拼凑法需要较高的变形能力,通过对已有解析式进行变形,找出对应关系;

    (2)换元法是解决此类问题在逻辑上最容易接受的一种方法,通过换元找出对应关系;

    (3)待定系数法在应用时,一定要弄清函数类型,切不可盲目下手.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知f(x)=
    (3-a)x-1(x＜1)
    logax(x≥1)
    是R上的增函数，那么a的取值范围是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2014•达州一模）已知f(x)=
    (3-a)x-a
    logax
    (x＜1)
    (x≥1)
    是（-∞，+∞）上的增函数，则a的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)=
    (3-a)x+1，x＜1
    ax，x≥1
    是R上增函数，那么a的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知f(x)=
    3(x＞0)
    4(x=0)
    5(x＜0)
    ，则f[f（-1）]=
     
    ．

    查看答案和解析>>

    同步练习册答案