
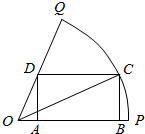 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的运动点,ABCD是扇形的内接矩形.记∠COP=α,求当角α取何值时,矩形ABCD的面积最大?并求出这个最大面积.分析 (1)先用所给的角表示AB,BC,即可将矩形的面积表示出来,建立三角函数模型;
(2)根据所建立的模型利用三角函数的性质求最值.
解答 解:(1)如图,在Rt△OBC中,OB=cosα,BC=sinα,
在Rt△OAD中,$\frac{DA}{OA}$=tan60°=$\sqrt{3}$,所以OA=$\frac{\sqrt{3}}{3}$DA=$\frac{\sqrt{3}}{3}$BC=$\frac{\sqrt{3}}{3}$sinα.
所以AB=OB-OA=cosα$\frac{\sqrt{3}}{3}$sinα.
设矩形ABCD的面积为S,则S=AB•BC=(cosα$\frac{\sqrt{3}}{3}$sinα)sinα=sinαcosα$\frac{\sqrt{3}}{3}$sin2α
=$\frac{1}{2}$sin2α+$\frac{\sqrt{3}}{6}$cos2α-$\frac{\sqrt{3}}{6}$=$\frac{1}{\sqrt{3}}$($\frac{\sqrt{3}}{2}$sin2α+$\frac{1}{2}$cos2α)-$\frac{\sqrt{3}}{6}$
=$\frac{\sqrt{3}}{3}$sin(2α+$\frac{π}{6}$)-$\frac{\sqrt{3}}{6}$(0<α<$\frac{π}{3}$).
(2)由于0<α<$\frac{π}{3}$,所以当2α+$\frac{π}{6}$=$\frac{π}{2}$,即α=$\frac{π}{6}$时,S最大=$\frac{\sqrt{3}}{3}$-$\frac{\sqrt{3}}{6}$=$\frac{\sqrt{3}}{6}$.
因此,当α=$\frac{π}{6}$时,矩形ABCD的面积最大,最大面积为$\frac{\sqrt{3}}{6}$.
点评 本题考查在实际问题中建立三角函数模型,求解问题的关键是根据图形建立起三角模型,将三角模型用所学的恒等式变换公式进行化简.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{kπ}{2}+\frac{π}{4}$ | B. | $\frac{kπ}{2}$ | C. | kπ+$\frac{π}{4}$ | D. | kπ-$\frac{π}{4}$(其中k∈Z) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com