
【题目】某中学对高三年级的学生进行体质测试,已知高三、一班共有学生30人,测试立定跳远的成绩用茎叶图表示如下(单位:![]() ):
):
|
|
| 男 |
| 女 |
|
|
|
|
|
7 | 16 | 5 | 7 | 8 | 9 | 9 | ||||
9 | 8 | 17 | 1 | 8 | 4 | 5 | 2 | 9 | ||
3 | 5 | 6 | 18 | 0 | 2 | 7 | 5 | 4 | ||
1 | 2 | 4 | 19 | 0 | 1 | |||||
1 8 5 | 20 21 22 |
男生成绩不低于![]() 的定义为“合格”,成绩低于
的定义为“合格”,成绩低于![]() 的定义为“不合格”;女生成绩不低于
的定义为“不合格”;女生成绩不低于![]() 的定义为“合格”,成绩低于
的定义为“合格”,成绩低于![]() 的定义为“不合格”.
的定义为“不合格”.
(1) 求女生立定跳远成绩的中位数;
(2) 若在男生中按成绩是否合格进行分层抽样,抽取6个人,求抽取成绩“合格”的男生人数;
(3) 若从(2)问所抽取的6人中任选2人,求这2人中恰有1人成绩“合格”的概率.
【答案】(1)166.5cm(2)4人(3)![]()
【解析】
(1)由茎叶图能求出女生立定跳远成绩的中位数.
(2)男生成绩“合格”的有8人,“不合格”的有4人,用分层抽样的方法,能求出其中成绩“合格”的学生应抽取的人数.
(3)由(2)可知6人中,4人合格,2人不合格,设合格学生为A,B,C,D,不合格学生为![]() ,利用列举法能求出这2人中恰有1人成绩“合格”的概率.
,利用列举法能求出这2人中恰有1人成绩“合格”的概率.
(1) 女生立定跳远成绩的中位数![]() cm.
cm.
(2)男生中成绩“合格”和“不合格”人数比为![]() ,用分层抽样的方法抽取6个人,
,用分层抽样的方法抽取6个人,
则抽取成绩“合格”人数为4人;
(3)由(2)设成绩“合格”的4人为A,B,C,D,成绩“不合格”的2人为![]() ,从中选出2人有(A,B),(A,C),(A,D),(A,
,从中选出2人有(A,B),(A,C),(A,D),(A,![]() ),(A,
),(A,![]() ),(B,C),(B,D),(B,
),(B,C),(B,D),(B,![]() ),(B,
),(B,![]() ),(C,D),(C,
),(C,D),(C,![]() ),(C,
),(C,![]() ),(D,
),(D,![]() ),(D,
),(D,![]() ),(
),(![]() ),共15种,
),共15种,
其中恰有1人成绩“合格”的有(A,![]() ),(A,
),(A,![]() ),(B,
),(B,![]() ),(B,
),(B,![]() ),(C,
),(C,![]() ),(C,
),(C,![]() ),(D,
),(D,![]() ),(D,
),(D,![]() ),共8种,故所求事件概率为
),共8种,故所求事件概率为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了研究某种微生物的生长规律,研究小组在实验室对该种微生物进行培育实验.前三天观测的该微生物的群落单位数量分别为12,16,24.根据实验数据,用y表示第![]() 天的群落单位数量,某研究员提出了两种函数模型;①
天的群落单位数量,某研究员提出了两种函数模型;①![]() ;②
;②![]() ,其中a,b,c,p,q,r都是常数.
,其中a,b,c,p,q,r都是常数.
(1)根据实验数据,分别求出这两种函数模型的解析式;
(2)若第4天和第5天观测的群落单位数量分别为40和72,请从这两个函数模型中选出更合适的一个,并计算从第几天开始该微生物群落的单位数量超过1000.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行硏究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
温差x( | 8 | 11 | 13 | 12 | 10 |
发芽数y(颗) | 22 | 27 | 31 | 35 | 26 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均不小于27”的概率.
(2)若选取的是3月1日与3月5日的两组数据,请根据3月2日至3月4日的数据,求出y关于x的线性回归方程![]() .
.
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(参考公式:回归直线的方程是![]() ,其中
,其中 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 不等式
不等式![]() ,其中
,其中![]() .
.
(1)试求不等式的解集![]() ;
;
(2)对于不等式的解集![]() ,若满足
,若满足![]() (其中
(其中![]() 为整数集).试探究集合
为整数集).试探究集合![]() 能否为有限集?若能,求出使得集合
能否为有限集?若能,求出使得集合![]() 中元素个数最少时
中元素个数最少时![]() 的取值范围,并用列举法表示集合
的取值范围,并用列举法表示集合![]() ;若不能,请说明理由.
;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知点
中,已知点![]() ,点
,点![]() ,
,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上的动点,且满足
上的动点,且满足![]() .
.
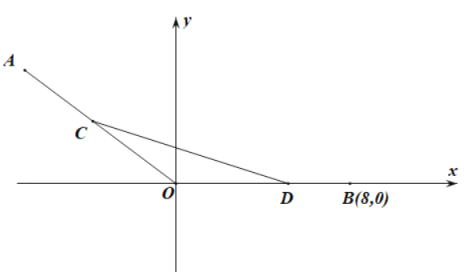
(1)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)设点![]() 的坐标为
的坐标为![]() ,求
,求![]() 的外接圆的一般方程,并求
的外接圆的一般方程,并求![]() 的外接圆所过定点的坐标.
的外接圆所过定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,由四个全等的直角三角形和一个正方形构成.现有五种不同的颜色可供涂色,要求相邻的区域不能用同一种颜色,则不同的涂色方案有( )

A.180B.192C.420D.480
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为6,且椭圆
的长轴长为6,且椭圆![]() 与圆
与圆![]() 的公共弦长为
的公共弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点P(0,1)作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,
,![]() ,试判断在
,试判断在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为以
为以![]() 为底边的等腰三角形,若存在,求出点
为底边的等腰三角形,若存在,求出点![]() 的横坐标的取值范围;若不存在,请说明理由.
的横坐标的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2名女生、4名男生排成一排,求:
(1)2名女生不相邻的不同排法共有多少种?
(2)女生甲必须排在女生乙的左边(不一定相邻)的不同排法共有多少种?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com