
分析 由sinθ,cosθ≠0,可得数列{an}是以sinθ为首项,以cosθ为公比的等比数列,由数列的极限等于$\sqrt{3}$列式,再由辅助角公式化积后求得θ.
解答 解:∵sinθ,cosθ≠0,∴数列{an}是以sinθ为首项,以cosθ为公比的等比数列,
则$\underset{lim}{n→∞}$(a1+a2+…+an)=$\frac{sinθ}{1-cosθ}$=$\sqrt{3}$,
即sinθ+$\sqrt{3}cosθ=\sqrt{3}$.
∴2($\frac{1}{2}$sinθ+$\frac{\sqrt{3}}{2}$cosθ)=$\sqrt{3}$,即sin(θ+$\frac{π}{3}$)=$\frac{\sqrt{3}}{2}$.
∴θ+$\frac{π}{3}$=$\frac{π}{3}+2kπ$或$θ+\frac{π}{3}=\frac{2π}{3}+2kπ,k∈Z$.
则θ=2kπ(舍)或$θ=\frac{π}{3}+2kπ,k∈Z$.
点评 本题考查数列递推式,考查了等比关系的确定,训练了数列极限的求法,是中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北石家庄一中高一下期末数学(理)试卷(解析版) 题型:选择题
已知椭圆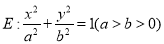 的右焦点为
的右焦点为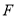 .短轴的一个端点为
.短轴的一个端点为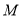 ,直线
,直线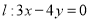 交椭圆
交椭圆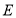 于
于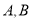 两点.若
两点.若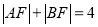 ,点
,点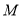 到直线
到直线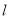 的距离不小于
的距离不小于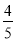 ,则椭圆
,则椭圆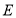 的离心率的取值范围是
的离心率的取值范围是
A.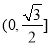 B.
B.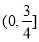 C.
C.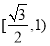 D.
D.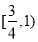
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com