
【题目】已知三棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,则三棱锥
,则三棱锥![]() 外接球的体积为( )
外接球的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】分析:由几何关系首先求得外接球的半径,然后利用球的体积公式求解体积的大小即可.
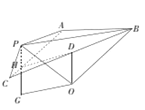
详解:如图取BC的中点为D,
显然三棱锥P-ABC的外接球的球心O一定在过点D,且垂直于面ABC的垂线DO上.
设OD=h,在△PAC中,AC=4,PA=![]() ,PC=
,PC=![]() ,
,
利用余弦定理得cos∠PCA=![]() .
.
在△PAC中过P作PH⊥AC,所以PH⊥平面ABC,易求PH=CH=1.
在△CDH中,CH=1,CD=![]() ,
,![]() ,
,
以DO与DH为邻边作矩形DOGH,
因为三棱锥P-ABC的外接球的球心为O,
所以OP=OB,OP2=(h+1)2+5,OB2=(![]() )2+h2,
)2+h2,
那么![]() ,解得OD=h=1,
,解得OD=h=1,
可得外接球的半径OB=3,![]() .
.
本题选择B选项.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
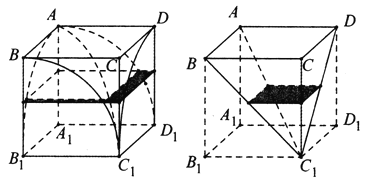
【题目】为推导球的体积公式,刘徽制造了一个牟合方盖(在一个正方体内作两个互相垂直的内切圆柱,这两个圆柱的公共部分叫做牟合方盖),但没有得到牟合方盖的体积.200年后,祖暅给出牟合方盖的体积计算方法,其核心过程被后人称为祖暅原理:缘幂势既同,则积不容异.意思是,夹在两个平行平面间的两个几何体被平行于这两个平行平面的任意平面所截,如果截面的面积总相等,那么这两个几何体的体积也相等.现在截取牟合方盖的八分之一,它的外切正方体![]() 的棱长为1,如图所示,根据以上信息,则该牟合方盖的体积为( )
的棱长为1,如图所示,根据以上信息,则该牟合方盖的体积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国互联网信息技术的发展,网络购物已经成为许多人消费的一种重要方式,某市为了了解本市市民的网络购物情况,特委托一家网络公示进行了网络问卷调查,并从参与调查的10000名网民中随机抽取了200人进行抽样分析,得到了下表所示数据:
经常进行网络购物 | 偶尔或从不进行网络购物 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
(1)依据上述数据,能否在犯错误的概率不超过![]() 的前提下认为该市市民进行网络购物的情况与性别有关?
的前提下认为该市市民进行网络购物的情况与性别有关?
(2)现从所抽取的女性网民中利用分层抽样的方法再抽取![]() 人,从这
人,从这![]() 人中随机选出
人中随机选出![]() 人赠送网络优惠券,求出选出的
人赠送网络优惠券,求出选出的![]() 人中至少有两人是经常进行网络购物的概率;
人中至少有两人是经常进行网络购物的概率;
(3)将频率视为概率,从该市所有的参与调查的网民中随机抽取![]() 人赠送礼物,记经常进行网络购物的人数为
人赠送礼物,记经常进行网络购物的人数为![]() ,求
,求![]() 的期望和方差.
的期望和方差.
附:![]() ,其中
,其中![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且x≤0时, f(x)=-x+1
(1)求f(0),f(2);
(2)求函数f(x)的解析式;
(3)若f(a-1)<3,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子![]() 米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子
米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子![]() 米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过
米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过![]() 个直道与弯道的交接口
个直道与弯道的交接口![]() .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为![]() ,摔倒的概率均为
,摔倒的概率均为![]() .假定运动员只有在摔倒或到达终点时才停止滑行,现在用
.假定运动员只有在摔倒或到达终点时才停止滑行,现在用![]() 表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.

(1)求该运动员停止滑行时恰好已顺利通过![]() 个交接口的概率;
个交接口的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com