
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若![]() 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;
(3)证明:![]()
![]() 且
且![]()
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】如图,正三角形ABE与菱形ABCD所在的平面互相垂直,![]() ,
,![]() ,M是AB的中点,N是CE的中点.
,M是AB的中点,N是CE的中点.
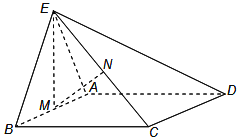
(1)求证:![]() ;
;
(2)求证:![]() 平面ADE;
平面ADE;
(3)求点A到平面BCE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国在欧洲的某孔子学院为了让更多的人了解中国传统文化,在当地举办了一场由当地人参加的中国传统文化知识大赛,为了了解参加本次大赛参赛人员的成绩情况,从参赛的人员中随机抽取![]() 名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如图所示,已知抽取的人员中成绩在[50,60)内的频数为3.
名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如图所示,已知抽取的人员中成绩在[50,60)内的频数为3.

(1)求![]() 的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
(2)已知抽取的![]() 名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取2人,记这4人中女士的人数为
名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取2人,记这4人中女士的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】勒洛三角形是具有类似圆的“定宽性”的曲线,它是由德国机械工程专家、机构运动学家勒洛首先发现,其作法是:以等边三角形每个顶点为圆心,以边长为半径,在另两个顶点间作一段弧,三段弧围成的曲边三角形就是勒洛三角形.如图中的两个勒洛三角形,它们所对应的等边三角形的边长比为![]() ,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为______.
,若从大的勒洛三角形中随机取一点,则此点取自小勒洛三角形内的概率为______.
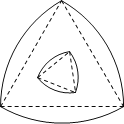
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知抛物线
中,已知抛物线![]()
![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离为6,点
的距离为6,点![]() 为其准线
为其准线![]() 上的任意一点,过点
上的任意一点,过点![]() 作抛物线
作抛物线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)当点![]() 在
在![]() 轴上时,证明:
轴上时,证明:![]() 为等腰直角三角形.
为等腰直角三角形.
(3)证明:![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 义乌国际马拉松赛,某校要从甲乙丙丁等
义乌国际马拉松赛,某校要从甲乙丙丁等![]() 人中挑选
人中挑选![]() 人参加比赛,其中甲乙丙丁
人参加比赛,其中甲乙丙丁![]() 人中至少有
人中至少有![]() 人参加且甲乙不同时参加,丙丁也不同时参加,则不同的报名方案有( )
人参加且甲乙不同时参加,丙丁也不同时参加,则不同的报名方案有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com