练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：极坐标与参数方程

    已知在一个极坐标系中点的极坐标为．

    （1）求出以为圆心，半径长为2的圆的极坐标方程（写出解题过程）并画出图形．

    （2）在直角坐标系中，以圆所在极坐标系的极点为原点，极轴为轴的正半轴建立直角坐标系，点是圆上任意一点， ， 是线段的中点，当点在圆上运动时，求点的轨迹的普通方程．

    【答案】（1）；（2）．

    【解析】试题分析：（1）设圆上任意一点 圆的极坐标方程，作图见解析；（2）设圆上任意一点，令，由， 是线段的中点 的参数方程为

    点的轨迹的普通方程为．

    试题解析： （1）如图，设圆上任意一点，则或，

    由余弦定理得，

    ∴圆的极坐标方程，作图．

    （2）在直角坐标系中，点的坐标为，可设圆上任意一点，

    又令，由， 是线段的中点，

    ∴的参数方程为即（为参数）．

    ∴点的轨迹的普通方程为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数恰有两个零点，则实数的取值范围为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某文化创意公司开发出一种玩具（单位：套）进行生产和销售．根据以往经验，每月生产x套玩具的成本p由两部分费用（单位：元）构成：．固定成本（与生产玩具套数x无关），总计一百万元；b．生产所需的直接总成本．

    （1）问：该公司每月生产玩具多少套时，可使得平均每套所需成本费用最少？此时每套玩具的成本费用是多少？

    （2）假设每月生产出的玩具能全部售出，但随着x的增大，生产所需的直接总成本在急剧增加，因此售价也需随着x的增大而适当增加．设每套玩具的售价为q元，（）．若当产量为15000套时利润最大，此时每套售价为300元，试求、b的值．（利润=销售收入-成本费用）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

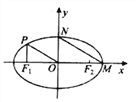
    【题目】如图，椭圆的左、右焦点为，右顶点为，上顶点为，若， 与轴垂直，且.

    （1）求椭圆方程；

    （2）过点且不垂直于坐标轴的直线与椭圆交于两点，已知点，当时，求满足的直线的斜率的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

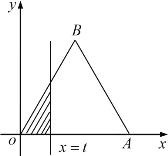
    【题目】如图，在直角坐标系中，已知点，，直线将分成两部分，记左侧部分的多边形为.设各边长的平方和为，各边长的倒数和为.

    （Ⅰ） 分别求函数和的解析式；

    （Ⅱ）是否存在区间，使得函数和在该区间上均单调递减？若存在，求 的最大值；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知多面体的直观图（图1）和它的三视图（图2），

    （1）在棱上是否存在点，使得平面？若存在，求的值，并证明你的结论；若不存在，说明理由；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）若不等式的解集为，求实数的值；

    （2）在（1）的条件下，若存在实数使成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足.

    （1）若数列是等差数列，求的值；

    （2）当时，求数列的前项和；

    （3）若对任意，都有成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，某旅游区拟建一主题游乐园，该游乐区为五边形区域ABCDE，其中三角形区域ABE为主题游乐区，四边形区域为BCDE为休闲游乐区，AB、BC，CD，DE，EA，BE为游乐园的主要道路（不考虑宽度）．.

    （I）求道路BE的长度；

    （Ⅱ）求道路AB，AE长度之和的最大值．

    查看答案和解析>>

    同步练习册答案