
【题目】[2018·郴州期末]已知三棱锥![]() 中,
中,![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,垂足为
,垂足为![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
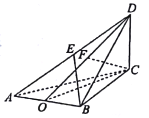
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)要证线面垂直,一般先证线线垂直,这可由![]() 和
和![]() 是等边三角形及O是AB中点易得;
是等边三角形及O是AB中点易得;
(2)要求直线与平面所成的角,一种方法作出线面角的平面角,然后解三角形得结论,也可建立空间直角坐标系,如解析中的坐标系,写出各点坐标,求出直线的方向向量与平面的法向量,由方向向量与法向量的夹角与直线和平面所成角互余可得.
试题解析:
(1)证明:∵![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 是等边三角形.
是等边三角形.
又![]() 是等边三角形.
是等边三角形.
∴![]() 是
是![]() 中点,
中点,![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)解:由(1)知![]() ,平面
,平面![]() 平面
平面![]() .
.
因为平面![]() 与平面
与平面![]() 的交线为
的交线为![]() .
.
∵![]() 平面
平面![]() .∴
.∴![]() .
.
又等边![]() 面积为
面积为![]() ,∴
,∴![]()
又![]() ,∴
,∴ ![]() 是
是![]() 中点.
中点.
如图建立空间直角坐标系![]() ,
,
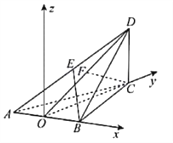
![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则
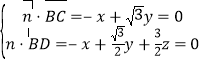 ,取
,取![]() ,则
,则![]() ,
,![]() .
.
即平面![]() 的一个法向量为
的一个法向量为![]() .
.
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为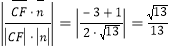 .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 的焦点F在直线
的焦点F在直线![]() 上。
上。
(Ⅰ)求抛物线C的方程。
(Ⅱ)过点![]() 做互相垂直的两条直线
做互相垂直的两条直线![]() 与曲线C交于A,B两点,
与曲线C交于A,B两点,![]() 与曲线C交于E,F两点,线段AB、EF的中点分别为M、N,求证:直线MN过定点P,并求出定点P的坐标。
与曲线C交于E,F两点,线段AB、EF的中点分别为M、N,求证:直线MN过定点P,并求出定点P的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为打赢打好脱贫攻坚战,实现建档立卡贫困人员稳定增收,某地区把特色养殖确定为脱贫特色主导产业,助力乡村振兴.现计划建造一个室内面积为![]() 平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留
平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留![]() 米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为
米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为![]() 米,如图所示.
米,如图所示.

(1)将两个养殖池的总面积![]() 表示
表示![]() 为的函数,并写出定义域;
为的函数,并写出定义域;
(2)当温室的边长![]() 取何值时,总面积
取何值时,总面积![]() 最大?最大值是多少?
最大?最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() 图像上任意一点
图像上任意一点![]() 处的切线的斜率
处的切线的斜率![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若对于区间![]() 上任意两个不相等的实数
上任意两个不相等的实数![]() 都有
都有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,若椭圆上一点
,若椭圆上一点![]() 满足
满足![]() ,且椭圆
,且椭圆![]() 过点
过点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]()
![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 轴的垂线,交椭圆
轴的垂线,交椭圆![]() 于
于![]() ,求证:
,求证: ![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-![]() 中,
中,![]() 平面ABC,D,E,F,G分别为
平面ABC,D,E,F,G分别为![]() ,AC,
,AC,![]() ,
,![]() 的中点,AB=BC=
的中点,AB=BC=![]() ,AC=
,AC=![]() =2.
=2.

(Ⅰ)求证:AC⊥平面BEF;
(Ⅱ)求二面角B-CD-C1的余弦值;
(Ⅲ)证明:直线FG与平面BCD相交.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以“你我中国梦,全民建小康”为主题、“社会主义核心价值观”为主线,为了了解![]() 两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度,对
两个地区的观众对2018年韩国平昌冬奥会准备工作的满意程度,对![]() 地区的100名观众进行统计,统计结果如下:
地区的100名观众进行统计,统计结果如下:
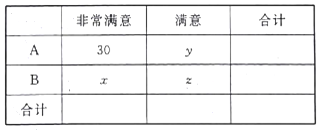
在被调查的全体观众中随机抽取1名“非常满意”的人是![]() 地区的概率为0.45,且
地区的概率为0.45,且![]() .
.
(Ⅰ)现从100名观众中用分层抽样的方法抽取20名进行问卷调查,则应抽取“满意”的![]() 地区的人数各是多少?
地区的人数各是多少?
(Ⅱ)在(Ⅰ)抽取的“满意”的观众中,随机选出3人进行座谈,求至少有两名是![]() 地区观众的概率?
地区观众的概率?
(Ⅲ)完成上述表格,并根据表格判断是否有![]() 的把握认为观众的满意程度与所在地区有关系?
的把握认为观众的满意程度与所在地区有关系?
附: 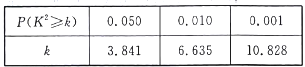 ,
, 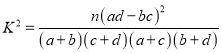 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足:对于任意
满足:对于任意![]() 均为数列
均为数列![]() 中的项,则称数列
中的项,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 的前
的前![]() 项和
项和![]() ,求证:数列
,求证:数列![]() 为“
为“![]() 数列”;
数列”;
(2)若公差为![]() 的等差数列
的等差数列![]() 为“
为“![]() 数列”,求
数列”,求![]() 的取值范围;
的取值范围;
(3)若数列![]() 为“
为“![]() 数列”,
数列”,![]() ,且对于任意
,且对于任意![]() ,均有
,均有![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com