
分析 (1)由f(x)=$\frac{1-x}{1+x}$,先求出f(2),再计算f(f(2))的值.
(2)由已知得$\left\{\begin{array}{l}{\frac{1-{a}^{2}}{1+{a}^{2}}=-\frac{3}{5}}\\{{2}^{a-1}<1}\end{array}\right.$,由此能求出a.
(3)由已知得当n为奇数时,${f}_{n}(x)=\frac{1-x}{1+x}$;n为偶数时,fn(x)=x.由此能求出结果.
(4)由已知得t=a2-2a+$\frac{13}{3}$=(a-1)2+$\frac{10}{3}$≥$\frac{10}{3}$,g(x)=f(x)•φ(x)=-|x-2|${\;}^{\frac{1}{2}}$,由此能判断g(1,2),g(2,5),g(t)的大小关系.
解答 解:(1)∵f(x)=$\frac{1-x}{1+x}$,∴f(2)=$\frac{1-2}{1+2}$=-$\frac{1}{3}$,
∴f(f(2))=f(-$\frac{1}{3}$)=$\frac{1+\frac{1}{3}}{1-\frac{1}{3}}$=2.
(2)∵实数a满足f(a2)=$-\frac{3}{5}$,且lg2a-1<0,
∴$\left\{\begin{array}{l}{\frac{1-{a}^{2}}{1+{a}^{2}}=-\frac{3}{5}}\\{{2}^{a-1}<1}\end{array}\right.$,
解得a=-2.
(3)∵f1(x)=f(x)=$\frac{1-x}{1+x}$(x≠-1),对于一切正整数n,都有fn+1(x)=f1(fn(x)),
∴${f}_{2}(x)=\frac{1-\frac{1-x}{1+x}}{1+\frac{1-x}{x+x}}$=x,${f}_{3}(x)=\frac{1-x}{1+x}$,
∴当n为奇数时,${f}_{n}(x)=\frac{1-x}{1+x}$;n为偶数时,fn(x)=x.
∵f3(x)=f4(x),
∴$\frac{1-x}{1+x}=x$,整理,得x2+2x-1=0,解得$x=-1±\sqrt{2}$,
∴f2012(x)=x=-1$±\sqrt{2}$.
(4)∵φ(x)=$\frac{1+x}{x-1}|x-2{|}^{\frac{1}{2}}$(x≠1),函数g(x)=f(x)•φ(x),t=a2-2a+$\frac{13}{3}$(a∈R),
∴t=a2-2a+$\frac{13}{3}$=(a-1)2+$\frac{10}{3}$≥$\frac{10}{3}$,
g(x)=f(x)•φ(x)=-|x-2|${\;}^{\frac{1}{2}}$,
∴g(1.2)=-|1.2-2|${\;}^{\frac{1}{2}}$=-$\sqrt{0.8}$,
g(2.5)=-|2.5-2|${\;}^{\frac{1}{2}}$=-$\sqrt{0.5}$,
g(t)=-|t-2|${\;}^{\frac{1}{2}}$≤-$\sqrt{\frac{4}{3}}$,
∴g(2.5)>g(1.2)>g(t).
点评 本题考查函数值的求法,考查实数a的值的求法,考查三个数的大小的判断,是中档题,解题时要认真审题,注意函数性质的合理运用.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
 若a,b是两个正整数,阅读如图的伪代码.
若a,b是两个正整数,阅读如图的伪代码.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
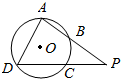 如图,四边形ABCD是⊙O的内接四边形,延长AB和DC相交于点P,若$\frac{PB}{PA}$=$\frac{1}{2}$,$\frac{PC}{PD}$=$\frac{1}{3}$,则$\frac{BC}{AD}$的值为$\frac{\sqrt{6}}{6}$.
如图,四边形ABCD是⊙O的内接四边形,延长AB和DC相交于点P,若$\frac{PB}{PA}$=$\frac{1}{2}$,$\frac{PC}{PD}$=$\frac{1}{3}$,则$\frac{BC}{AD}$的值为$\frac{\sqrt{6}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com