练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设二次函数f(x)＝x2＋2x＋b的图象与两坐标轴有三个交点，经过这三个交点的圆记为圆C．

    (1)求实数b的取值范围；

    (2)求圆C的方程；

    (3)问圆C是否经过某定点(其坐标与b无关)？若是，求出定点的坐标；若不是，说明理由．

    答案：
    解析：

    　　解：(1)令x＝0，得抛物线与y轴交点是(0，b)．因为f(x)的图象与两坐标轴有三个交点，所以b≠0．令f(x)＝x2＋2x＋b＝0，则Δ＝4－4b＞0，解得b＜1．所以b的取值范围是(－∞，0)∪(0，1)．

    　　(2)设圆C的方程为x2＋y2＋Dx＋Ey＋F＝0．令y＝0，得x2＋Dx＋F＝0．由题意知，该方程与x2＋2x＋b＝0的根相同，故D＝2，F＝b．令x＝0，得y2＋Ey＋F＝0．由题意知，此方程有一个根为b，代入得E＝－b－1．所以圆C的方程为x2＋y2＋2x－(b＋1)y＋b＝0．

    　　(3)将圆C的方程变形为(1－y)b＋(x2＋y2＋2x－y)＝0．由于b的任意性，得解得．所以圆C必过定点(0，1)和(－2，1)．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：浙江省杭州高中2006-2007学年度第一学期高三年级第三次月考　数学试题(文) 题型：044

    解答题：解答应写出文字说明，证明过程或演算步骤．

    设二次函数f(x)＝ax2＋bx＋c，(a，b，c∈R)满足下列条件：

    ①当x∈R时，f(x)的最小值为0，且f(x－1)＝f(－x－1)成立；

    ②当x∈(0，5)时，x≤f(x)≤2|x－1|＋1恒成立．

    (1)

    求f(1)的值

    (2)

    求f(x)的解析式

    (3)

    求最大的实数t，使得当x∈[1，3]时，f(x＋t)≤x恒成立．

    查看答案和解析>>

    科目：高中数学 来源：2014届云南省高一下学期期末数学试卷（解析版） 题型：解答题

    （12分）（1）设x、y、zR，且x＋y＋z＝1，求证x2＋y2＋z2≥；

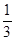    （2）设二次函数f (x)＝ax2＋bx＋c （a＞0），方程f (x)－x＝0有两个实根x1，x2，

    且满足：0＜x1＜x2＜，若x(0，x1)。

    求证：x＜f (x)＜x1

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设二次函数f(x)＝ax2＋bx+c(a＞0），方程f(x)－x＝0的两根x1、x2满足0＜x1＜x2＜．

    （1）当x∈（0，x1）时，证明x＜f(x)＜x1；

     

    （2）设函数f(x)的图象关于直线x=x0对称；

    证明：x0＜

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设二次函数f(x)＝x2+ax+a，方程f(x)-x＝0的两根x1和x2满足0<x1<x2<1.

    （1）求实数a的取值范围；

    （2）试比较f(0)·f(1)-f(0)与的大小，并说明理由

    查看答案和解析>>

    同步练习册答案