正项数列
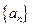
满足
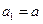
,
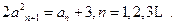
(1)若
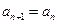
,求
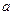
的值;
(2)当
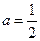
时,证明:
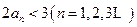
;
(3)设数列
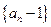
的前
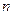
项之积为
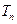
,若对任意正整数
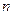
,总有
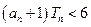
成立,求
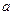
的取值范围
(1)因为
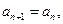
所以
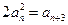
,解得
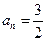
或
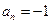
(舍去)
由
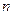
的任意性知,
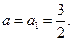
……………3分
(2)反证法:假设
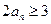
……………4分
即
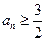
,则
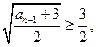
得
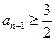
依此类推,
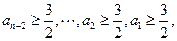
这与
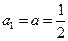
矛盾。
所以假设不成立,则
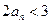
……………7分
(3)由题知,当
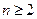
时,
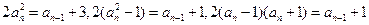
,
所以
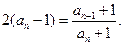
同理有
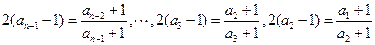
将上述
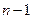
个式子相乘,得
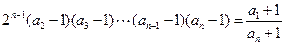
,
即
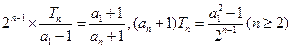
……………11分
当
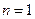
时,
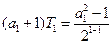
也成立,
所以
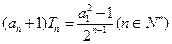
……………12分
从而要使
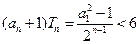
对任意的
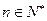
恒成立,
只要使
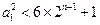
对任意的
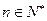
恒成立即可。
因为数列
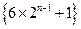
单调递增,所以
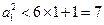
……………13分
即
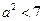
所以实数
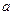
的取值范围是
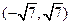
又a>0, 所以实数
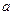
的取值范围是
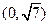
………14分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)数列
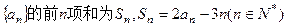
(1)若数列
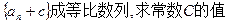
(2)求数列
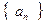
的通项公式
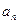
(3)数列
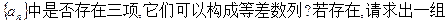
适合条件的项;若不存在,请说明理由
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分16分)
设数列
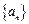
满足
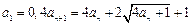
,令
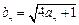
.
⑴试判断数列
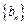
是否为等差数列?并说明理由;
⑵若
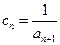
,求
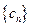
前
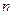
项的和
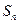
;
⑶是否存在
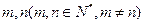
使得
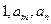
三数成等比数列?
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分10分)
已知数列
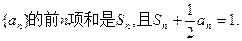
(1)求数列
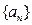
的通项公式;
(2)设
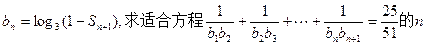
的值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)已知等差数列{
an2}中,首项
a12=1,公差
d=1,
an>0,
n∈
N*.
(1)求数列{
an}的通项公式;
(2)设
bn=
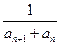
,数

列{
bn}的前
n项和为
Tn;
①求
T120; ②求证:

当
n>3时,

2
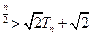
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)
在数列
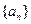
中,
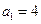
且对任意
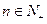
均有:
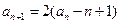
(I)证明数列
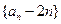
是等比数列;
(II)求数列
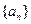
的通项公式;
(Ⅲ)求证:
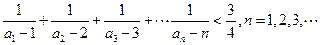
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分16分)
设数列
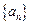
的前
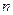
项和为
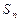
,若对任意
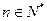
,都有
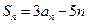
.
⑴求数列
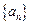
的首项;
⑵求证:数列
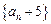
是等比数列,并求数列
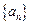
的通项公式;
⑶数列
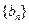
满足
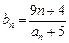
,问是否存在
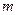
,使得
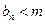
恒成立?如果存在,求出
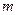
的值,如果不存在,说明理由.
查看答案和解析>>

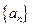 满足
满足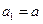 ,
,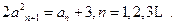
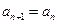 ,求
,求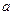 的值;
的值;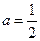 时,证明:
时,证明: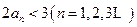 ;
;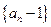 的前
的前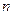 项之积为
项之积为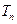 ,若对任意正整数
,若对任意正整数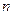 ,总有
,总有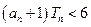 成立,求
成立,求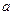 的取值范围
的取值范围 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案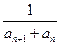 ,数
,数 列{bn}的前n项和为Tn;
列{bn}的前n项和为Tn; 当n>3时,
当n>3时,  2
2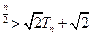
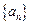 的前
的前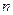 项和为
项和为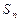 ,若对任意
,若对任意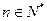 ,都有
,都有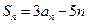 .
.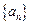 的首项;
的首项;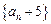 是等比数列,并求数列
是等比数列,并求数列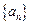 的通项公式;
的通项公式;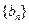 满足
满足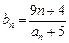 ,问是否存在
,问是否存在 ,使得
,使得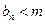 恒成立?如果存在,求出
恒成立?如果存在,求出 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.