
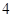 为周期的函数
为周期的函数 ,其中
,其中 。若方程
。若方程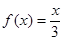 恰有5个实数解,则
恰有5个实数解,则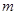 的取值范围为 ( )
的取值范围为 ( ) A.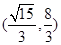 | B.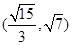 | C.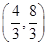 | D.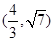 . . |
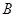
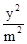 =1(y≥0),
=1(y≥0),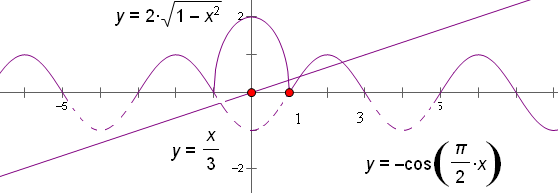
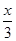 与第二个椭圆(x-4)2+
与第二个椭圆(x-4)2+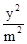 =1(y≥0)相交,而与第三个半椭圆(x-8)2+
=1(y≥0)相交,而与第三个半椭圆(x-8)2+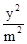 ="1" (y≥0)无公共点时,方程恰有5个实数解,
="1" (y≥0)无公共点时,方程恰有5个实数解,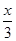 代入(x-4)2+
代入(x-4)2+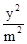 =1(y≥0)得,(9m2+1)x2-72m2x+135m2=0,令t=9m2(t>0),
=1(y≥0)得,(9m2+1)x2-72m2x+135m2=0,令t=9m2(t>0),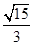 ,
,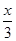 代入第三个椭圆方程(x-8)2+
代入第三个椭圆方程(x-8)2+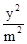 ="1" (y≥0),由△<0可计算得 m<
="1" (y≥0),由△<0可计算得 m<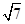 ,
,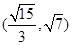 ,故选B。
,故选B。

 中考解读考点精练系列答案
中考解读考点精练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com