
ΓΨΧβΡΩΓΩΈ“Ο«ΙζΦ“’ΐ¥Π”ΎάœΝδΜ·…γΜα÷–Θ§άœ”–Υυ“ά“≤ «’ΰΗ°ΒΡΟώ…ζΙΛ≥ΧΘ°Ρ≥ –Ι≤”–ΜßΦ°»ΥΩΎ400ΆρΘ§Τδ÷–άœ»ΥΘ®ΡξΝδ60ΥξΦΑ“‘…œΘ©»Υ ΐ‘Φ”–66ΆρΘ§ΈΣΝΥΝΥΫβάœ»ΥΟ«ΒΡΫΓΩΒΉ¥ΩωΘ§’ΰΗ°¥”άœ»Υ÷–ΥφΜζ≥ι»Γ600»Υ≤ΔΈ·Ά–“ΫΝΤΜζΙΙΟβΖ―ΈΣΥϊΟ«Ϋχ––ΫΓΩΒΤάΙάΘ§ΫΓΩΒΉ¥ΩωΙ≤Ζ÷ΈΣ≤ΜΡήΉ‘άμΓΔ≤ΜΫΓΩΒ…–ΡήΉ‘άμΓΔΜυ±ΨΫΓΩΒΓΔΫΓΩΒΥΡΗωΒ»ΦΕΘ§≤Δ“‘80ΥξΈΣΫγœόΖ÷≥…ΝΫΗω»ΚΧεΫχ––Ά≥ΦΤΘ§―υ±ΨΖ÷≤Φ±Μ÷ΤΉς≥…»γΆΦ±μΘΚ 
Θ®1Θ©»τ≤…”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®‘Ό¥”―υ±Ψ÷–ΒΡ≤ΜΡήΉ‘άμΒΡάœ»Υ÷–≥ι»Γ8»ΥΫχ“Μ≤ΫΝΥΫβΥϊΟ«ΒΡ…ζΜνΉ¥ΩωΘ§‘ρΝΫΗω»ΚΧε÷–Ης”Π≥ι»ΓΕύ…Ό»ΥΘΩ
Θ®2Θ©ΙάΥψΗΟ –80ΥξΦΑ“‘…œ≥Λ’Ώ’Φ»Ϊ –ΜßΦ°»ΥΩΎΒΡΑΌΖ÷±»ΘΜ
Θ®3Θ©ΨίΆ≥ΦΤΗΟ –¥σ‘Φ”–ΈεΖ÷÷°“ΜΒΡΜßΦ°άœ»ΥΈόΙΧΕ® ’»κΘ§’ΰΗ°ΦΤΜ°ΈΣ’β≤ΩΖ÷άœ»ΥΟΩ‘¬ΖΔΖ≈…ζΜν≤ΙΧυΘ§±ξΉΦ»γœ¬ΘΚ ΔΌ80ΥξΦΑ“‘…œ≥Λ’ΏΟΩ»ΥΟΩ‘¬ΖΔΖ≈…ζΜν≤ΙΧυ200‘ΣΘΜ
ΔΎ80Υξ“‘œ¬άœ»ΥΟΩ»ΥΟΩ‘¬ΖΔΖ≈…ζΜν≤ΙΧυ120‘ΣΘΜ
Δέ≤ΜΡήΉ‘άμΒΡάœ»ΥΟΩ»ΥΟΩ‘¬ΕνΆβΖΔΖ≈…ζΜν≤ΙΧυ100‘ΣΘ° ‘ΙάΦΤ’ΰΗ°÷¥––¥ΥΦΤΜ°ΒΡΡξΕ»‘ΛΥψΘ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©ΫβΘΚ ΐΨί’ϊάμ»γœ¬±μΘΚ
ΫΓΩΒΉ¥Ωω | ΫΓΩΒ | Μυ±ΨΫΓΩΒ | ≤ΜΫΓΩΒ…–ΡήΉ‘άμ | ≤ΜΡήΉ‘άμ |
80ΥξΦΑ“‘…œ | 20 | 45 | 20 | 15 |
80Υξ“‘œ¬ | 200 | 225 | 50 | 25 |
¥”ΆΦ±μ÷–÷Σ≤…”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®‘Ό¥”―υ±Ψ÷–ΒΡ≤ΜΡήΉ‘άμΒΡάœ»Υ÷–≥ι»Γ8»ΥΫχ“Μ≤ΫΝΥΫβΥϊΟ«ΒΡ…ζΜνΉ¥ΩωΘ§
80ΥξΦΑ“‘…œ”Π≥ι»ΓΘΚ8ΓΝ ![]() =3»ΥΘ§
=3»ΥΘ§
80Υξ“‘…œ”Π≥ι»ΓΘΚ8ΓΝ ![]() =5»ΥΘ°
=5»ΥΘ°
Θ®2Θ©ΫβΘΚ‘Ύ600»Υ÷–80ΥξΦΑ“‘…œ≥Λ’Ώ‘Ύάœ»Υ÷–’Φ±»ΈΣΘΚ
![]() Θ§
Θ§
”Ο―υ±ΨΙάΦΤΉήΧεΘ§80ΥξΦΑ“‘…œ≥Λ’Ώ’ΦΜßΦ°»ΥΩΎΒΡΑΌΖ÷±»ΈΣ ![]() Γ÷16.67%Θ°
Γ÷16.67%Θ°
Θ®3Θ©ΫβΘΚ”Ο―υ±ΨΙάΦΤΉήΧεΘ§…η»Έ“ΜΜßΦ°άœ»ΥΟΩ‘¬œμ ήΒΡ…ζΜν≤Ι÷ζΈΣX‘ΣΘ§
PΘ®X=0Θ©= ![]() Θ§
Θ§
PΘ®X=120Θ©= ![]() =
= ![]() Θ§
Θ§
PΘ®X=200Θ©= ![]() =
= ![]() Θ§
Θ§
PΘ®X=220Θ©= ![]() =
= ![]() Θ§
Θ§
PΘ®X=300Θ©= ![]() =
= ![]() Θ§
Θ§
‘ρΥφΜζ±δΝΩXΒΡΖ÷≤ΦΝ–ΈΣΘΚ
X | 0 | 120 | 200 | 220 | 300 |
P |
|
|
|
|
|
EX= ![]() =28Θ§
=28Θ§
»Ϊ –άœ»ΥΒΡΉή‘ΛΥψΈΣ28ΓΝ12ΓΝ66ΓΝ104=2.2176ΓΝ108‘ΣΘ°
’ΰΗ°÷¥––¥ΥΦΤΜ°ΒΡΡξΕ»‘ΛΥψ‘ΦΈΣ2.2176“Ύ‘Σ
ΓΨΫβΈωΓΩΘ®1Θ©¥”ΆΦ±μ÷–«σ≥ω≤ΜΡήΉ‘άμΒΡ80ΥξΦΑ“‘…œ≥Λ’Ώ’Φ±»Θ§”…¥ΥΡή«σ≥ω”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®‘Ό¥”―υ±Ψ÷–ΒΡ≤ΜΡήΉ‘άμΒΡάœ»Υ÷–≥ι»Γ8»ΥΫχ“Μ≤ΫΝΥΫβΥϊΟ«ΒΡ…ζΜνΉ¥ΩωΘ§ΝΫΗω»ΚΧε÷–Ης”Π≥ι»ΓΕύ…Ό»ΥΘ°Θ®2Θ©«σ≥ω‘Ύ600»Υ÷–80ΥξΦΑ“‘…œ≥Λ’Ώ‘Ύάœ»Υ÷–’Φ±»Θ§”Ο―υ±ΨΙάΦΤΉήΧεΘ§Ρή«σ≥ω80ΥξΦΑ“‘…œ≥Λ’Ώ’ΦΜßΦ°»ΥΩΎΒΡΑΌΖ÷±»Θ°Θ®3Θ©”Ο―υ±ΨΙάΦΤΉήΧεΘ§…η»Έ“ΜΜßΦ°άœ»ΥΟΩ‘¬œμ ήΒΡ…ζΜν≤Ι÷ζΈΣX‘ΣΘ§‘ρXΒΡΩ…Ρή»Γ÷ΒΈΣ0Θ§120Θ§200Θ§220Θ§300Θ§Ζ÷±π«σ≥ωœύ”ΠΒΡΗ≈¬ Θ§”…¥ΥΡή«σ≥ωΥφΜζ±δΝΩXΒΡΖ÷≤ΦΝ–ΓΔEXΘ§¥”ΕχΡήΙάΦΤ’ΰΗ°÷¥––¥ΥΦΤΜ°ΒΡΡξΕ»‘ΛΥψΘ°


 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§‘ΎΕύΟφΧεA1B1D1-DCBA÷–,ΥΡ±Ώ–ΈAA1B1BΘ§ADD1A1,ABCDΨυΈΣ’ΐΖΫ–ΈΘ§EΈΣB1D1ΒΡ÷–Βψ Θ§ΙΐA1 Θ§ DΘ§EΒΡΤΫΟφΫΜCD 1”ΎFΓΘ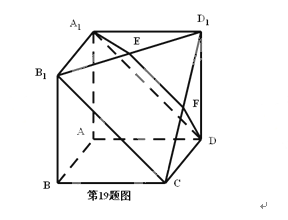
Θ®1Θ©÷ΛΟςΘΚEFΓΈB1C
Θ®2Θ©«σΕΰΟφΫ«E-A1D-B1ΒΡ”ύœ“ΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΉφ≥ε÷°÷°Ή”Ήφï€ «Έ“ΙζΡœ±±≥· ±¥ζΈΑ¥σΒΡΩΤ―ßΦ“Θ§Υϊ‘Ύ ΒΦυΒΡΜυ¥Γ…œΧα≥ωΝΥΧεΜΐΦΤΥψΒΡ‘≠άμΘΚΓΑΟί ΤΦ»Ά§Θ§‘ρΜΐ≤Μ»ί“λΓ±.“βΥΦ «Θ§»γΙϊΝΫΗωΒ»ΗΏΒΡΦΗΚΈΧε ‘ΎΆ§ΗΏ¥ΠΫΊΒΟΒΡΫΊΟφΟφΜΐΚψΒ»Θ§Ρ«Ο¥’βΝΫΗωΦΗΚΈΧεΒΡΧεΜΐœύΒ».¥ΥΦ¥Ήφ≠άμ.άϊ”Ο’βΗω‘≠άμ«σ«ρΒΡΧεΜΐ ±Θ§–η“ΣΙΙ‘λ“ΜΗω¬ζΉψΧθΦΰΒΡΦΗΚΈΧεΘ§“―÷ΣΗΟΦΗΚΈΧε»ΐ ”ΆΦ »γΆΦΥυ ΨΘ§”Ο“ΜΗω”κΗΟΦΗΚΈΧεΒΡœ¬ΒΉΟφΤΫ––œύΨύΈΣ h(0<h<2) ΒΡΤΫΟφΫΊΗΟΦΗΚΈΧεΘ§‘ρΫΊΟφΟφΜΐΈΣ Θ® Θ©
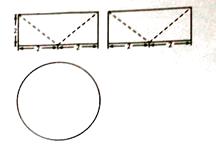
A.![]()
B.![]()
C.![]()
D.Π–Θ®4-h2Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΓςABC÷–Θ§…η±ΏaΘ§bΘ§cΥυΕ‘ΒΡΫ«ΈΣAΘ§BΘ§CΘ§«“AΘ§BΘ§CΕΦ≤Μ «÷±Ϋ«Θ§Θ®bc©¹8Θ©cosA+accosB=a2©¹b2 Θ° Θ®ΔώΘ©»τb+c=5Θ§«σbΘ§cΒΡ÷ΒΘΜ
Θ®ΔρΘ©»τ ![]() Θ§«σΓςABCΟφΜΐΒΡΉν¥σ÷ΒΘ°
Θ§«σΓςABCΟφΜΐΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΩΦ ‘≤βΤά÷–Θ§≥Θ”ΟΡ―Ε»«ζœΏΆΦά¥Φλ≤βΧβΡΩΒΡ÷ ΝΩΘ§“ΜΑψά¥ΥΒΘ§»ΪΨμΒΟΖ÷ΗΏΒΡ―ß…ζΘ§‘ΎΡ≥ΒάΧβΡΩ…œΒΡ¥πΕ‘¬ “≤”ΠΫœΗΏΘ§»γΙϊ «Ρ≥¥Έ ΐ―ß≤β ‘―Ι÷αΧβΒΡΒΎ1ΓΔ2Έ ΒΟΖ÷Ρ―Ε»«ζœΏΆΦΘ§ΒΎ1ΓΔ2Έ ¬ζΖ÷ΨυΈΣ6Ζ÷Θ§ΆΦ÷–ΚαΉχ±ξΈΣΖ÷ ΐΕΈΘ§ΉίΉχ±ξΈΣΗΟΖ÷ ΐΕΈΒΡ»ΪΧεΩΦ…ζ‘ΎΒΎ1ΓΔ2Έ ΒΡΤΫΨυΡ―Ε»Θ§‘ρœ¬Ν–ΥΒΖ®’ΐ»ΖΒΡ «Θ® Θ© 
A.¥ΥΧβΟΜ”–ΩΦ…ζΒΟ12Ζ÷
B.¥ΥΧβΒΎ1Έ ±»ΒΎ2Έ ΗϋΡή«χΖ÷―ß…ζ ΐ―ß≥…Φ®ΒΡΚΟ”κΜΒ
C.Ζ÷ ΐ‘Ύ[40Θ§50Θ©ΒΡΩΦ…ζ¥Υ¥σΧβΒΡΤΫΨυΒΟΖ÷¥σ‘ΦΈΣ4.8Ζ÷
D.»ΪΧεΩΦ…ζΒΎ1Έ ΒΡΒΟΖ÷±ξΉΦ≤ν–Γ”ΎΒΎ2Έ ΒΡΒΟΖ÷±ξΉΦ≤ν
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐfΘ®xΘ©=eax+ΠΥlnxΘ§Τδ÷–aΘΦ0Θ§0ΘΦΠΥΘΦ ![]() Θ§e «Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐ
Θ§e «Ή‘»ΜΕ‘ ΐΒΡΒΉ ΐ
Θ®1Θ©«σ÷ΛΘΚΚ· ΐfΘ®xΘ©”–ΝΫΗωΦΪ÷ΒΒψΘΜ
Θ®2Θ©»τ©¹eΓήaΘΦ0Θ§«σ÷ΛΘΚΚ· ΐfΘ®xΘ©”–Έ®“ΜΝψΒψΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΚ· ΐ ![]() ΒΡΉν¥σ÷ΒΈΣ2Θ§ΥϋΒΡΉν–Γ’ΐ÷ήΤΎΈΣ2Π–Θ° Θ®ΔώΘ©«σΚ· ΐfΘ®xΘ©ΒΡΫβΈω ΫΘΜ
ΒΡΉν¥σ÷ΒΈΣ2Θ§ΥϋΒΡΉν–Γ’ΐ÷ήΤΎΈΣ2Π–Θ° Θ®ΔώΘ©«σΚ· ΐfΘ®xΘ©ΒΡΫβΈω ΫΘΜ
Θ®ΔρΘ©»τgΘ®xΘ©=cosxfΘ®xΘ©Θ§«σgΘ®xΘ©‘Ύ«χΦδ ![]() …œΒΡΉν¥σ÷ΒΚΆΉν–Γ÷ΒΘ°
…œΒΡΉν¥σ÷ΒΚΆΉν–Γ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»τΚ· ΐfΘ®xΘ©= ![]() ”–Ήν¥σ÷ΒΘ§‘ρ Β ΐaΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
”–Ήν¥σ÷ΒΘ§‘ρ Β ΐaΒΡ»Γ÷ΒΖΕΈß «Θ® Θ©
A.![]()
B.![]()
C.[©¹2Θ§+ΓόΘ©
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΟϊάΚ«ρ‘ΥΕ·‘±‘Ύ7≥Γ±»»ϋ÷–ΒΡΒΟΖ÷«ιΩω»γΨΞ“ΕΥυ ΨΘ§ ![]() ΦΉΓΔ
ΦΉΓΔ ![]() ““Ζ÷±π±μ ΨΦΉΓΔ““ΝΫ»ΥΒΡΤΫΨυΒΟΖ÷Θ§‘ρœ¬Ν–≈–Εœ’ΐ»ΖΒΡ «Θ® Θ©
““Ζ÷±π±μ ΨΦΉΓΔ““ΝΫ»ΥΒΡΤΫΨυΒΟΖ÷Θ§‘ρœ¬Ν–≈–Εœ’ΐ»ΖΒΡ «Θ® Θ© 
A.![]() ΦΉΘΨ
ΦΉΘΨ ![]() ““ Θ§ ΦΉ±»““ΒΟΖ÷Έ»Ε®
““ Θ§ ΦΉ±»““ΒΟΖ÷Έ»Ε®
B.![]() ΦΉΘΨ
ΦΉΘΨ ![]() ““ Θ§ ““±»ΦΉΒΟΖ÷Έ»Ε®
““ Θ§ ““±»ΦΉΒΟΖ÷Έ»Ε®
C.![]() ΦΉΘΦ
ΦΉΘΦ ![]() ““ Θ§ ΦΉ±»““ΒΟΖ÷Έ»Ε®
““ Θ§ ΦΉ±»““ΒΟΖ÷Έ»Ε®
D.![]() ΦΉΘΦ
ΦΉΘΦ ![]() ““ Θ§ ““±»ΦΉΒΟΖ÷Έ»Ε®
““ Θ§ ““±»ΦΉΒΟΖ÷Έ»Ε®
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com