分析:法一:(1)由题设知,欲使得段CC1上求一点E使得A1C⊥面BED,又B1C是A1C在外侧面上的投影,故必有B1C⊥BE,可证得△BCB1~△BCE,进而可求得CE:BC=1:2,求出CE的值.
(2)点A到平面A1B1C的距离可转化为点B到平面A1B1C的距离,即求BF;
(3)连接DF可证得∠EDF就是DE与平面A1B1C所成角,正弦值易求
法二:本题具备建立空间坐标系的条件,故可用空间向量法求解
(1)证A1C⊥面BED问题可转化为A1C与平面的法向量共线的问题,
(2)点A到平面A1B1C的距离转化成向量BC在平面法向量上的投影的长度来解决;
(3)求直线DE与平面A1B1C所成角的正弦值可转化为求DE与平面法向量的余弦的绝对值问题.
解答:解:法一:(1)∵A
1C⊥面BED,∴A
1C⊥BE,
由A
1B
1⊥面BB
1C
1C知,A
1C为面BB
1C
1C的斜线,B
1C为其射影,∴B
1C⊥BE.
∵△BCB
1~△BCE,∴
==?CE=.
(2)可以证明AB∥面A
1B
1C,所以点A到平面A
1B
1C的距离与点B到平面A
1B
1C的距离相等;
又BE⊥A
1C,BE⊥B
1C,∴BE⊥面A
1B
1C,∴线段BF的长就是所求的距离.在△BCB
1中可以求得
BF=.
(3)连接DF有(2)知EF⊥面A
1B
1C,所以∠EDF就是DE与平面A
1B
1C所成角.在△BCE中求得
EF=,
△DCE中求得
DE=,∴
sin∠EDF==.
法二:本题还可以用向量法求解如下:
(1)根据正四棱棱柱性质,建立空间直角坐标系A-xyz,
B(1,0,0),D(0,1,0),C(1,1,0),B
1(1,0,2),A
1(0,0,2).
设E(1,1,z),
∵A
1C⊥面BED,
∴A
1C⊥BE,∴
•=0,
∴(1,1,-2)•(0,1,z)=0,
∴
z=CE=.
(2)由(1)可以证明BE⊥面A
1B
1C,所以
=
(0,1,)就是面A
1B
1C的法向量,
所以点A到平面A
1B
1C的距离
d=||=.
(3)设直线DE与平面A
1B
1C所成角为θ,则
sinθ=||=.
点评:本是考点是点、线、面间的距离计算,综合考查了线面垂直,点到面的距离、线面角,由两种方法解题过程可以看出,解决本题用空间向量方法较好,用空间向量求线面角、面面角、点到面的距离等立体几何问题大降低了解决问题时的思维难度,但其缺点也很明显,即运算量稍大,解完本题请比较一下两种方法的优劣.

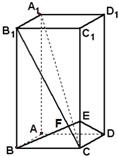 如图,己知正四棱棱柱AC1中,AB=BC=1,BB1=2,连接B1C和A1C
如图,己知正四棱棱柱AC1中,AB=BC=1,BB1=2,连接B1C和A1C

 如图,己知正四棱棱柱AC1中,AB=BC=1,BB1=2,连接B1C和A1C
如图,己知正四棱棱柱AC1中,AB=BC=1,BB1=2,连接B1C和A1C