
(本题12分)直线l:y=kx+1与双曲线C: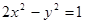 的右支交于不同的两点A,B.
的右支交于不同的两点A,B.
(Ⅰ)求实数k的取值范围;
(Ⅱ)是否存在实数k,使得以线段AB为直径的圆经过双曲线C的右焦点F?若存在,求出k的值;若不存在,说明理由.
(Ⅰ)-2<k<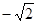 ;
;
(Ⅱ)k=-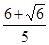 时,使得以线段AB为直径的圆经过双曲线C的右焦点.
时,使得以线段AB为直径的圆经过双曲线C的右焦点.
解析试题分析:(Ⅰ)由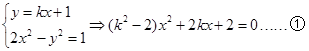
据题意: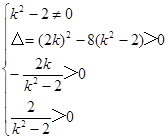 解得-2<k<
解得-2<k<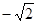 ……………5分
……………5分
(Ⅱ)设A,B两点的坐标分别为(x1,y1),(x2,y2), 则由①式得: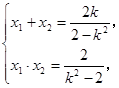
假设存在实数k,使得以线段AB为直径的圆过双曲线C的右焦点F(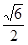 ,0),则FA
,0),则FA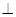 FB.
FB.
即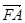 ·
·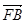 =0,(x1-
=0,(x1-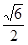 )(x2-
)(x2-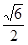 )+y1y2=0,
)+y1y2=0,
(x1-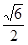 )(x2-
)(x2-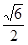 )+(kx1+1)(kx2+1)=0,
)+(kx1+1)(kx2+1)=0,
(1+k2)x1 x2+(k-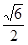 )(x1+ x2)+
)(x1+ x2)+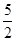 =0,
=0,
∴(1+k2)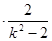 +(k-
+(k-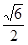 )·
)·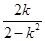 +
+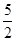 =0,
=0,
∴5k2+2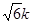 -6=0
-6=0
∴k=-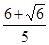 或k=
或k=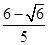 ,
,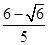
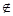 (-2,-
(-2,- )(舍去)
)(舍去)
∴k=-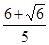 时,使得以线段AB为直径的圆经过双曲线C的右焦点.…………………12分
时,使得以线段AB为直径的圆经过双曲线C的右焦点.…………………12分
考点:本题主要考查直线与双曲线的位置关系。
点评:中档题,涉及直线与圆锥曲线的位置关系问题,往往要利用韦达定理。存在性问题,往往从假设存在出发,运用题中条件探寻得到存在的是否条件具备。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题12分)已知椭圆 的离心率为
的离心率为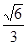 ,
, 为椭圆的右焦点,
为椭圆的右焦点,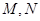 两点在椭圆
两点在椭圆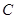 上,且
上,且 ,定点
,定点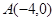 。
。
(1)若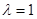 时,有
时,有 ,求椭圆
,求椭圆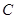 的方程;
的方程;
(2)在条件(1)所确定的椭圆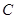 下,当动直线
下,当动直线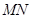 斜率为k,且设
斜率为k,且设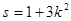 时,试求
时,试求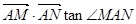 关于S的函数表达式f(s)的最大值,以及此时
关于S的函数表达式f(s)的最大值,以及此时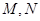 两点所在的直线方程。
两点所在的直线方程。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知抛物线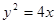 及点
及点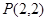 ,直线
,直线 的斜率为1且不过点P,与抛物线交于A,B两点。
的斜率为1且不过点P,与抛物线交于A,B两点。
(1) 求直线 在
在 轴上截距的取值范围;
轴上截距的取值范围;
(2) 若AP,BP分别与抛物线交于另一点C,D,证明:AD、BC交于定点。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知点P(4,4),圆C: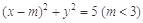 与椭圆E:
与椭圆E: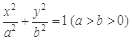 有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.
有一个公共点A(3,1),F1、F2分别是椭圆的左、右焦点,直线PF1与圆C相切.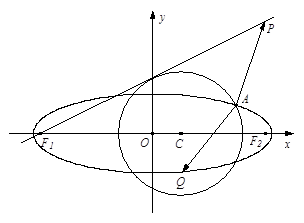
(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求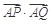 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
.已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线方程为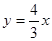 ,右焦点
,右焦点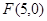 ,双曲线的实轴为
,双曲线的实轴为 ,
,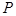 为双曲线上一点(不同于
为双曲线上一点(不同于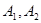 ),直线
),直线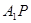 ,
,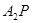 分别与直线
分别与直线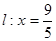 交于
交于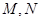 两点
两点
(1)求双曲线的方程;
(2)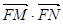 是否为定值,若为定值,求出该值;若不为定值,说明理由。
是否为定值,若为定值,求出该值;若不为定值,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某海域有 、
、 两个岛屿,
两个岛屿, 岛在
岛在 岛正东4海里处。经多年观察研究发现,某种鱼群洄游的路线是曲线
岛正东4海里处。经多年观察研究发现,某种鱼群洄游的路线是曲线 ,曾有渔船在距
,曾有渔船在距 岛、
岛、 岛距离和为8海里处发现过鱼群。以
岛距离和为8海里处发现过鱼群。以 、
、 所在直线为
所在直线为 轴,
轴, 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。
(1)求曲线 的标准方程;(6分)
的标准方程;(6分)
(2)某日,研究人员在 、
、 两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同),
两岛同时用声纳探测仪发出不同频率的探测信号(传播速度相同), 、
、 两岛收到鱼群在
两岛收到鱼群在 处反射信号的时间比为
处反射信号的时间比为 ,问你能否确定
,问你能否确定 处的位置(即点
处的位置(即点 的坐标)?(8分)
的坐标)?(8分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知椭圆的中心是坐标原点 ,焦点在x轴上,离心率为
,焦点在x轴上,离心率为 ,又椭圆上任一点到两焦点的距离和为
,又椭圆上任一点到两焦点的距离和为 ,过点M(0,
,过点M(0, )与x轴不垂直的直线
)与x轴不垂直的直线 交椭圆于P、Q两点.
交椭圆于P、Q两点.
(1)求椭圆的方程;
(2)在y轴上是否存在定点N,使以PQ为直径的圆恒过这个点?若存在,求出N的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)过点(1,0)直线 交抛物线
交抛物线 于A(x1,y1),B(x2,y2)两点,抛物线的顶点是
于A(x1,y1),B(x2,y2)两点,抛物线的顶点是 .
.
(ⅰ)证明: 为定值;
为定值;
(ⅱ)若AB中点横坐标为2,求AB的长度及 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com