
【题目】选修4—5:不等式选讲
已知函数![]() .
.
(1)当![]() 时,解不等式
时,解不等式![]() ;
;
(2)若存在实数![]() ,使得不等式
,使得不等式![]() 成立,求实
成立,求实![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)根据绝对值定义,将原不等式等价转化为三个不等式组,求它们的并集得原不等式的解集(2)不等式有解问题往往转化为对应函数最值问题:![]() ,由绝对值三角不等式得||x﹣3|﹣|x﹣a||≤|(x﹣3)﹣(x﹣a)|=|a﹣3|,即转化为解不等式:
,由绝对值三角不等式得||x﹣3|﹣|x﹣a||≤|(x﹣3)﹣(x﹣a)|=|a﹣3|,即转化为解不等式:![]() ,再利用绝对值定义求解得解集
,再利用绝对值定义求解得解集
试题解析:(1)当a=2时,f(x)=|x﹣3|﹣|x﹣2|,
当x≥3时,![]() ,即为
,即为![]() ,即
,即![]() 成立,则有x≥3;
成立,则有x≥3;
当x≤2时,![]() 即为
即为![]() ,即
,即![]() ,解得x∈;
,解得x∈;
当2<x<3时,![]() 即为
即为![]() ,解得,
,解得,![]() ,则有
,则有![]() .
.
则原不等式的解集为![]() 即为
即为![]() ;
;
(2)由绝对值不等式的性质可得||x﹣3|﹣|x﹣a||≤|(x﹣3)﹣(x﹣a)|=|a﹣3|,
即有![]() 的最大值为|a﹣3|.
的最大值为|a﹣3|.
若存在实数x,使得不等式![]() 成立,则有
成立,则有![]()
即![]() 或
或![]() ,即有
,即有![]() ∈或
∈或![]() ≤
≤![]() .所以
.所以![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】已知直线l:mx﹣y=1,若直线l与直线x+m(m﹣1)y=2垂直,则m的值为_____,动直线l:mx﹣y=1被圆C:x2﹣2x+y2﹣8=0截得的最短弦长为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的右焦点为
的右焦点为![]() ,
,![]() 为圆
为圆![]() 与椭圆
与椭圆![]() 的一个公共点,
的一个公共点,![]() .
.
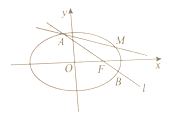
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)如图,过![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为点
为点![]() 关于
关于![]() 轴的对称点.
轴的对称点.
(1)求证:![]() ;
;
(2)试问过![]() ,
,![]() 的直线是否过定点?若是,请求出该定点;若不是,请说明理由.
的直线是否过定点?若是,请求出该定点;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
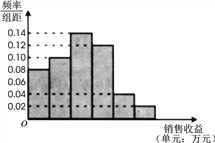
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入![]() 万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从
万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从![]() 开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
开始计数的. [附:回归直线的斜率和截距的最小二乘估计公式分别为.]
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入![]() 万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入 | 1 | 2 | 3 | 4 | 5 |
销售收益 | 2 | 3 | 2 | 7 |
由表中的数据显示, ![]() 与
与![]() 之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出
之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出![]() 关于
关于![]() 的回归直线方程.
的回归直线方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,则下列命题中正确的个数是( )
,则下列命题中正确的个数是( )
①当![]() 时,函数
时,函数![]() 在
在![]() 上有最小值;②当
上有最小值;②当![]() 时,函数
时,函数![]() 在
在![]() 是单调增函数;③若
是单调增函数;③若![]() ,则
,则![]() ;④方程
;④方程![]() 可能有三个实数根.
可能有三个实数根.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列结论正确的是( )

A. 平面ABD⊥平面ABC B. 平面ADC⊥平面BDC
C. 平面ABC⊥平面BDC D. 平面ADC⊥平面ABC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com