
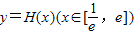 都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.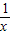 =
=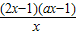 ,x>0,a>0,令F′(x)=0,则x=
,x>0,a>0,令F′(x)=0,则x= ,或
,或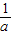 ,由此进行分类讨论,能求出函数F(x)的单调性.
,由此进行分类讨论,能求出函数F(x)的单调性.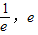 ]都有公共点.
]都有公共点.

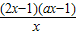 ,x>0,a>0,
,x>0,a>0, ,或
,或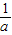 ,
,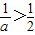 时,令F′(x)>0,解得0<x<
时,令F′(x)>0,解得0<x< ,或x>
,或x>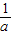 ;
; <x<
<x<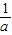 ;
; ),(
),(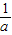 ,+∞)上单调递增,在(
,+∞)上单调递增,在( ,
, )单调递减.
)单调递减.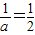 时,F′(x)≥0恒成立,
时,F′(x)≥0恒成立,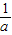
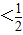 时,令F′(x)>0,解得0<x<
时,令F′(x)>0,解得0<x<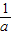 或x>
或x> ;
;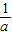 <x<
<x< ;
;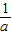 ),(
),( ,+∞)上单调递增,在(
,+∞)上单调递增,在(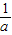 ,
, )单调递减.
)单调递减.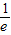 ,e)内变化时,H′(x),H(x)的变化情况如下表:
,e)内变化时,H′(x),H(x)的变化情况如下表:| x | 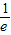 | (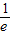 ,1) ,1) | 1 | (1,e) | e |
| H′(x) | - | + | |||
| H(x) | 2-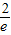 | ↘ | 极小值1 | ↗ | 2 |
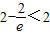 ,∴函数
,∴函数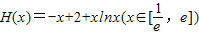 的值域为[1,2].
的值域为[1,2]. 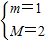 ,则对每一个t∈[m,M],
,则对每一个t∈[m,M],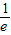 ,e]都有公共点;
,e]都有公共点;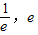 ]都没有公共点.
]都没有公共点.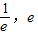 ]都有公共点.
]都有公共点.

科目:高中数学 来源: 题型:044
已知函数f(x)=x2-1(x≥1)的图象为 C1,曲线C2与C1关于直线y=x对称。
(1)求曲线C2的方程y=g(x);
(2)设函数y=g(x)的定义域为M,xl,x2∈ M,且xl≠x2,求证|g(x1)-g(x2)|<|x1-x2|;
(3)设A,B为曲线C2上任意不同两点,证明直线AB与直线y=x必相交。
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1)求曲线C2的方程y=g(x);
(2)设函数y=g(x)的定义域为M,xl,x2∈ M,且xl≠x2,求证|g(x1)-g(x2)|<|x1-x2|;
(3)设A,B为曲线C2上任意不同两点,证明直线AB与直线y=x必相交。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省淮北市高三第一次模拟考试文科数学 题型:解答题
.(本题满分13分)设函数 ,方程f(x)=x有唯一的解,
,方程f(x)=x有唯一的解,
已知f(xn)=xn+1(n∈N﹡)且f(xl)= .
.
(1)求证:数列{ )是等差数列;
)是等差数列;
(2)若 ,求Sn=b1+b2+b3+…+bn
,求Sn=b1+b2+b3+…+bn
(3)在(2)的条件下,是否存在最小正整数m,使得对任意n∈N﹡,有 成立,若存在,求出m的值;若不存在,请说明理由。
成立,若存在,求出m的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com