
分析 (1)求出f(x)的导数,配方,即可得到所求切线的斜率的最小值;
(2)由题意可设f(x)=(x-x1)(x-x2)(x-x3),求出导数,分别求出点A、B、C处切线斜率,再求倒数,化简即可得到所求和.
解答 解:(1)函数$f(x)={x^3}-{x^2}+({2\sqrt{2}-3})x+3-2\sqrt{2}$,
导数为f′(x)=3x2-2x+2$\sqrt{2}$-3
=3(x-$\frac{1}{3}$)2+2$\sqrt{2}$-$\frac{10}{3}$,
当x=$\frac{1}{3}$时,切线的斜率取得最小值2$\sqrt{2}$-$\frac{10}{3}$;
(2)可令f(x)=(x-x1)(x-x2)(x-x3),
f′(x)=(x-x2)(x-x3)+(x-x1)[(x-x2)+(x-x3)],
f′(x1)=(x1-x2)(x1-x3),f′(x2)=(x2-x1)(x2-x3),
f′(x3)=(x3-x1)(x3-x2),
可得点A、B、C处切线斜率倒数和为$\frac{1}{f′({x}_{1})}$+$\frac{1}{f′({x}_{2})}$+$\frac{1}{f′({x}_{3})}$
=$\frac{1}{{x}_{1}-{x}_{2}}$($\frac{1}{{x}_{1}-{x}_{3}}$-$\frac{1}{{x}_{2}-{x}_{3}}$)+$\frac{1}{({x}_{3}-{x}_{1})({x}_{3}-{x}_{2})}$
=$\frac{1}{{x}_{1}-{x}_{2}}$•$\frac{{x}_{2}-{x}_{1}}{({x}_{1}-{x}_{3})({x}_{2}-{x}_{3})}$+$\frac{1}{({x}_{3}-{x}_{1})({x}_{3}-{x}_{2})}$
=-$\frac{1}{({x}_{3}-{x}_{1})({x}_{3}-{x}_{2})}$+$\frac{1}{({x}_{3}-{x}_{1})({x}_{3}-{x}_{2})}$=0.
故答案为:(1)2$\sqrt{2}$-$\frac{10}{3}$,(2)0.
点评 本题考查导数的概念和应用:求切线的斜率,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<0或0<x<$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 参加书法班 | 未参加书法班 | |
| 参加演讲班 | 8 | 5 |
| 未参加演讲班 | 2 | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | 9 | C. | $\frac{{9\sqrt{3}}}{2}$ | D. | $\frac{{9\sqrt{3}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
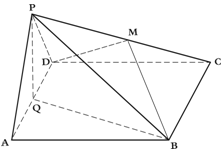 如图示,边长为4的正方形ABCD与正三角形ADP所在平面互相垂直,M、Q分别是PC,AD的中点.
如图示,边长为4的正方形ABCD与正三角形ADP所在平面互相垂直,M、Q分别是PC,AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
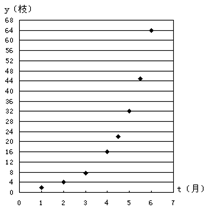 如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )
如图给出了红豆生长时间t(月)与枝数y(枝)的散点图:那么“红豆生南国,春来发几枝.”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好?( )| A. | 二次函数:y=2t2 | B. | 幂函数:y=t3 | ||
| C. | 指数函数:y=2t | D. | 对数函数:y=log2t |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com