
袋中装有大小相同的2个白球和3个黑球.
(1)采取放回抽样方式,从中依次摸出两个球,求两球颜色不同的概率;
(2)采取不放回抽样方式,从中依次摸出两个球,记 为摸出两球中白球的个数,
为摸出两球中白球的个数,
求 的期望.
的期望.
(1)两球颜色不同的概率是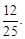 (2)摸出白球个数
(2)摸出白球个数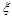 的期望是
的期望是 。
。
解析试题分析:(1)记 “摸出一球,放回后再摸出一个球,两球颜色不同”为事件A,
摸出一球得白球的概率为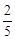 , 摸出一球得黑球的概率为
, 摸出一球得黑球的概率为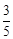 , 3分
, 3分
P(A)=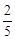 ×
×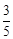 +
+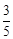 ×
×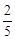 =
=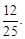
答:两球颜色不同的概率是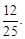 6分
6分
(2)由题知 可取0,1,2, 依题意得 7分
可取0,1,2, 依题意得 7分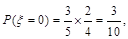
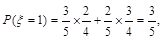
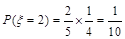 10分
10分
则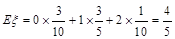 。
。
答: 摸出白球个数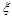 的期望是
的期望是 。. 12分
。. 12分
考点:随机变量的分布列及其数学期望,排列组合计算。
点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。本题对计算能力要求不太高,关键是理解分布列及数学期望的计算方法。


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:解答题
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.
(Ⅰ)求第4局甲当裁判的概率;
(Ⅱ)X表示前4局中乙当裁判的次数,求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为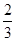 .现有10件产品,其中6件是一等品,4件是二等品.
.现有10件产品,其中6件是一等品,4件是二等品.
(1)随机选取1件产品,求能够通过检测的概率;
(2)随机选取3件产品,其中一等品的件数记为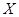 ,求
,求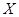 的分布列;
的分布列;
(3)随机选取3件产品,求这三件产品都不能通过检测的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某电视台综艺频道组织的闯关游戏,游戏规定前两关至少过一关才有资格闯第三关,闯关者闯第一关成功得3分,闯第二关成功得3分,闯第三关成功得4分.现有一位参加游戏者单独面第一关、第二关、第三关成功的概率分别为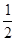 ,
,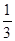 ,
,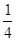 ,记该参加者闯三关所得总分为ζ.
,记该参加者闯三关所得总分为ζ.
(1)求该参加者有资格闯第三关的概率;
(2)求ζ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有甲、乙两个班,进行数学考试,按学生考试及格与不及格统计成绩后,得到如下的列联表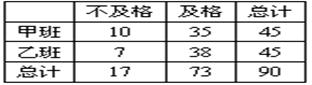
根据表中数据,你有多大把握认为成绩及格与班级有关?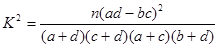
附表:
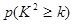 | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
(2)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图是一个从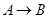 的”闯关”游戏.
的”闯关”游戏. 
规则规定:每过一关前都要抛掷一个在各面上分别标有1,2,3,4的均匀的正四面体.在过第n(n=1,2,3)关时,需要抛掷n次正四面体,如果这n次面朝下的数字之和大于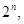 则闯关成功.
则闯关成功.
(1)求闯第一关成功的概率;
(2)记闯关成功的关数为随机变量X,求X的分布列和期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商店试销某种商品,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 概率 | 0.05 | 0.25 | 0.45 | 0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从某节能灯生产在线随机抽取100件产品进行寿命试验,按连续使用时间(单位:天)共分5组,得到频率分布直方图如图.
(I)以分组的中点资料作为平均数据,用样本估计该生产线所生产的节能灯的预期连续使用寿命;
(II)为了分析使用寿命差异较大的产品,从使用寿命低于200天和高于350天的产品中用分层抽样的方法共抽取6件,求样品A被抽到的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com