
【题目】对于函数y=f(x),若在其定义域内存在x0,使得x0f(x0)=1成立,则称函数f(x)具有性质M.
(1)下列函数中具有性质M的有____
①f(x)=﹣x+2
②f(x)=sinx(x∈[0,2π])
③f(x)=x![]() ,(x∈(0,+∞))
,(x∈(0,+∞))
④f(x)![]()
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,则实数a的取值范围是____.
【答案】①②④ a![]() 或a>0
或a>0
【解析】
(1)①因为f(x)=﹣x+2,若存在,则![]() ,解一元二次方程即可.②若存在,则
,解一元二次方程即可.②若存在,则![]() ,即
,即![]() ,再利用零点存在定理判断.③若存在,则
,再利用零点存在定理判断.③若存在,则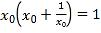 ,直接解方程.④若存在,则
,直接解方程.④若存在,则![]() ,即
,即![]() ,令
,令![]() ,再利用零点存在定理判断.
,再利用零点存在定理判断.
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,则ax(|x﹣2|﹣1)=1,x∈[﹣1,+∞)有解,将问题转化 :当![]() 时,
时,![]() 有解,当
有解,当![]() 时,
时,![]() 有解,分别用二次函数的性质求解.
有解,分别用二次函数的性质求解.
(1)①因为f(x)=﹣x+2,若存在,则![]() ,
,
即![]() ,所以
,所以![]() ,存在.
,存在.
②因为f(x)=sinx(x∈[0,2π]),若存在,则![]() ,
,
即![]() ,
,
令![]() ,
,
因为![]() ,
,
所以存在![]() .
.
③因为f(x)=x![]() ,(x∈(0,+∞)),若存在,则
,(x∈(0,+∞)),若存在,则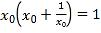 ,
,
即![]() ,所以不存在.
,所以不存在.
④因为f(x)![]() ,(x∈(0,+∞)),若存在,则
,(x∈(0,+∞)),若存在,则![]() ,
,
即![]() ,
,
令![]() ,
,
因为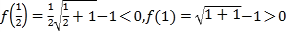 ,
,
所以存在![]() .
.
(2)若函数f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性质M,
则ax(|x﹣2|﹣1)=1,x∈[﹣1,+∞)有解,
当![]() 时,
时,![]() 有解,
有解,
令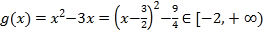 ,
,
所以![]() .
.
当![]() 时,
时,![]() 有解,
有解,
令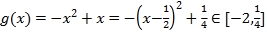 ,
,
所以![]() .
.
综上:实数a的取值范围是a![]() 或a>0.
或a>0.
故答案为:(1). ①②④ (2). a![]() 或a>0
或a>0


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知:在平面四边形ABCD中,![]() ,
,![]() ,
,![]() ,
,![]() (如图1),若将
(如图1),若将![]() 沿对角线BD折叠,使
沿对角线BD折叠,使![]() (如图2).请在图2中解答下列问题.
(如图2).请在图2中解答下列问题.
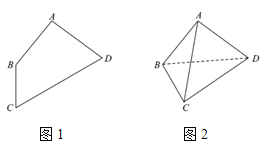
(1)证明:![]() ;
;
(2)求三棱锥![]() 的高.
的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),圆
为参数),圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的方程和圆
的方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 为圆
为圆![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的有( )
A.设正六棱锥的底面边长为1,侧棱长为![]() ,那么它的体积为
,那么它的体积为![]()
B.用斜二测法作△ABC的水平放置直观图得到边长为a的正三角形,则△ABC面积为![]()
C.三个平面可以将空间分成4,6,7或者8个部分
D.已知四点不共面,则其中任意三点不共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]:在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)判断曲线![]() ,
,![]() 是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com