
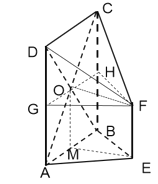
【题目】如图,在五面体![]() 中,侧面
中,侧面![]() 是正方形,
是正方形,![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 是正方形
是正方形![]() 对角线的交点
对角线的交点![]() ,
,![]() 且
且![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)若侧面![]() 与底面
与底面![]() 垂直,求五面体
垂直,求五面体![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明四边形
,证明四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,再利用直线与平面平行的判定定理可证明出
,再利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,将五面体
,将五面体![]() 分割为三棱柱
分割为三棱柱![]() 和四棱锥
和四棱锥![]() ,证明出
,证明出![]() 底面
底面![]() 和
和![]() 平面
平面![]() ,然后利用柱体和锥体体积公式计算出两个简单几何体的体积,相加可得出五面体
,然后利用柱体和锥体体积公式计算出两个简单几何体的体积,相加可得出五面体![]() 的体积.
的体积.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
![]() 侧面
侧面![]() 为正方形,且
为正方形,且![]() ,
,![]() 为
为![]() 的中点,
的中点,
又![]() 为
为![]() 的中点,
的中点,![]() 且
且![]() ,
,
![]() 且
且![]() ,
,![]() ,所以,四边形
,所以,四边形![]() 为平行四边形,
为平行四边形,![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,
,
![]() 四边形
四边形![]() 为正方形,
为正方形,![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 底面
底面![]() ,
,
易知![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,
![]() ,因此,
,因此,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知定义在区间![]() 上两个函数
上两个函数![]() 和
和![]() ,
,![]() ,
,![]()
![]() ,
,![]() .
.
(1)求函数![]() 的最大值
的最大值![]() ;
;
(2)若![]() 在区间
在区间![]() 单调,求实数
单调,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,若对于任意
时,若对于任意![]() ,总存在
,总存在![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构用“10分制”调查了各阶层人士对某次国际马拉松赛事的满意度,现从调查人群中随机抽取16名,如图茎叶图记录了他们的满意度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):

(1)指出这组数据的众数和中位数;
(2)若满意度不低于9.5分,则称该被调查者的满意度为“极满意”,求从这16人中随机选取3人,至少有2人满意度是“极满意”的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线方程为![]() 1,双曲线的一支上不同的三点A(x1,y1),B(6,
1,双曲线的一支上不同的三点A(x1,y1),B(6,![]() ),C(x2,y2)到焦点F(5,0)的距离成等差数列.
),C(x2,y2)到焦点F(5,0)的距离成等差数列.
(1)求m的值;
(2)试求x1+x2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宜昌大剧院和宜昌奥体中心将是人们健康生活的最佳场所,若两处在同一直角坐标系中的坐标分别为![]() ,
,![]() ;假设至喜长江大桥所在的直线方程为直线
;假设至喜长江大桥所在的直线方程为直线![]() .现为方便大家出行,计划在至喜长江大桥上的点p处新增一出口通往两地,要使从 处到两地的总路程最短.
.现为方便大家出行,计划在至喜长江大桥上的点p处新增一出口通往两地,要使从 处到两地的总路程最短.
(1)求点p的坐标.
(2)一中高二体育特长生小陶和小陈相约某周日上午8时到9时在宜昌奥体中心会面,并约定先到者应等候另一个人一刻钟,过时即可离去,求两人能会面的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《基础教育课程改革纲要(试行)》将“具有良好的心理素质”列入新课程的培养目标.为加强心理健康教育工作的开展,不断提高学生的心理素质,九江市某校高二年级开设了《心理健康》选修课,学分为2分.学校根据学生平时上课表现给出“合格”与“不合格”两种评价,获得“合格”评价的学生给予50分的平时分,获得“不合格”评价的学生给予30分的平时分,另外还将进行一次测验.学生将以“平时分×40%+测验分×80%”作为“最终得分”,“最终得分”不少于60分者获得学分.
该校高二(1)班选修《心理健康》课的学生的平时分及测验分结果如下:
测验分 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
平时分50分人数 | 0 | 1 | 1 | 3 | 4 | 4 | 2 |
平时分30分人数 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
(1)根据表中数据完成如下2×2列联表,并分析是否有95%的把握认为这些学生“测验分是否达到60分”与“平时分”有关联?
选修人数 | 测验分 达到60分 | 测验分 未达到60分 | 合计 |
平时分50分 | |||
平时分30分 | |||
合计 |
(2)用样本估计总体,若从所有选修《心理健康》课的学生中随机抽取5人,设获得学分人数为![]() ,求
,求![]() 的期望.
的期望.
附:![]() ,其中
,其中![]()
| 0.1 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879/p> | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com