设函数

则 ? ?
A.x= 为f(x)的极大值点 为f(x)的极大值点 | B.x= 为f(x)的极小值点 为f(x)的极小值点 |
| C.x=2为 f(x)的极大值点 | D.x=2为 f(x)的极小值点 |
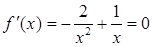
,得x="2," 因为当
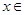
(0,2)时,
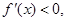
当
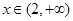
时,
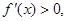
所以x=2为 f(x)的极小值点
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分14分)设函数
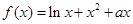
。
(1)若
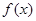
在

处取得极值,求

的值;
(2)若
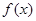
在定义域内为增函数,求

的取值范围;
(3)设
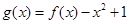
,当
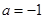
时,
求证:①

在其定义域内恒成立;
求证:②

。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数

.
(Ⅰ)当

时,如果函数

仅有一个零点,求实数

的取值范围;
(Ⅱ)当

时,试比较

与1的大小;
(Ⅲ)求证:


.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分14分)
已知
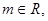
函数
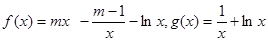
(Ⅰ)求
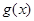
的最小值;
(Ⅱ)若

在
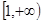
上为单调增函数,求实数
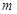
的取值范围;
(Ⅲ)证明:
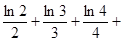
…
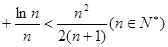
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设函数
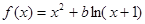
,其中
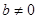
(1)当
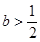
时,判断函数
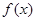
在定义域上的单调性;
(2)求
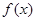
的极值点;
(3)证明对任意的正整数
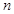
,不等式

都成立。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分12分)已知函数
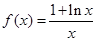
。
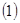
如果
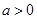
,函数在区间
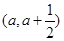
上存在极值,求实数a的取值范围;
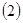
当
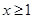
时,不等式
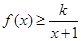
恒成立,求实数k的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分14分)设
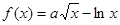
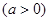
(1)若
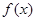
在
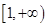
上递增,求
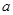
的取值范围;
(2)若
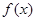
在
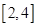
上的存在单调递减区间 ,求
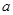
的取值范围
查看答案和解析>>

 则 ? ?
则 ? ? 为f(x)的极大值点
为f(x)的极大值点 为f(x)的极小值点
为f(x)的极小值点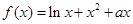 。
。 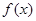 在
在 处取得极值,求
处取得极值,求 的值;
的值;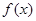 在定义域内为增函数,求
在定义域内为增函数,求 的取值范围;
的取值范围;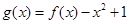 ,当
,当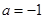 时,
时, 在其定义域内恒成立;
在其定义域内恒成立; 。
。