
【题目】设数列{an}的前n项和为Sn,且Sn=3an+1(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}满足![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:
(1)在已知等式![]() 中,令
中,令![]() 可求得
可求得![]() ,用
,用![]()
![]() 代替
代替![]() 可得
可得![]() ,两式相减,可得
,两式相减,可得![]() ,从而知
,从而知![]() 是等比数列,从而得通项公式;
是等比数列,从而得通项公式;
(2)由(1)可得![]() ,因此可用错位相减法求得其前
,因此可用错位相减法求得其前![]() 项和
项和![]() .
.
试题解析:
(Ⅰ)当n≥2时,an=Sn-Sn-1=3an+1-3an-1-1,
即2an=3an-1,所以![]() =
=![]() ,
,
当n=1时,a1=3a1+1,解得a1=-![]() .
.
所以数列{an}是以-![]() 为首项,
为首项,![]() 为公比的等比数列,即an=-
为公比的等比数列,即an=-![]() ×
×![]() .
.
(2)由(1)可得bn=-![]() ×
×![]()
所以Tn=3×![]() +5×
+5×![]() +…+(2n-1)
+…+(2n-1)![]()
![]() +(2n+1)
+(2n+1)![]() , ①
, ①
Tn=3×![]() +5×
+5×![]() +…+(2n-1)
+…+(2n-1)![]() +(2n+1)
+(2n+1)![]()
![]() , ②
, ②
则①—②,得![]() Tn=3×
Tn=3×![]() +2×
+2×![]() -(2n+1)
-(2n+1)![]()
![]() ,
,
化简整理可得Tn=5-![]()


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且在
,且在![]() 轴上的顶点分别为
轴上的顶点分别为![]() ,
,![]() .
.
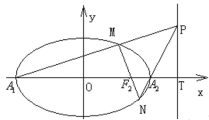
(1)求椭圆的方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为直线
为直线![]() 上异于点
上异于点![]() 的任一点,直线
的任一点,直线![]() 分别与椭圆交于
分别与椭圆交于![]() 点,试问直线
点,试问直线![]() 能否通过椭圆的焦点?若能,求出
能否通过椭圆的焦点?若能,求出![]() 的值,若不能,说明理由.
的值,若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)如图所示的茎叶图记录了甲、乙两组各四名同学的投篮命中次数, 乙组记录中有一个数据模糊,无法确认, 在图中以![]() 表示.
表示.

(Ⅰ)如果乙组同学投篮命中次数的平均数为![]() , 求
, 求![]() 及乙组同学投篮命中次数的方差;
及乙组同学投篮命中次数的方差;
(Ⅱ)在(Ⅰ)的条件下, 分别从甲、乙两组投篮命中次数低于10次的同学中,各随机选取一名, 记事件A:“两名同学的投篮命中次数之和为17”, 求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 与圆C相切,圆心C的坐标为
与圆C相切,圆心C的坐标为![]()
(1)求圆C的方程;
(2)设直线y=x+m与圆C交于M、N两点.
①若![]() ,求m的取值范围;
,求m的取值范围;
②若OM⊥ON,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年“十一”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,后得到如图的频率分布直方图.
,后得到如图的频率分布直方图.

(1)求这40辆小型车辆车速的众数和中位数的估计值;
(2)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆恰有一辆的概率.
的车辆恰有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孝感车天地关于某品牌汽车的使用年限![]() (年)和所支出的维修费用
(年)和所支出的维修费用![]() (千元)由如表的统计资料:
(千元)由如表的统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.1 | 3.4 | 5.9 | 6.6 | 7.0 |
(1)画出散点图并判断使用年限与所支出的维修费用是否线性相关;如果线性相关,求回归直线方程;
(2)若使用超过8年,维修费用超过1.5万元时,车主将处理掉该车,估计第10年年底时,车主是否会处理掉该车?
( )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,与直线
两点,与直线![]() 相交于点
相交于点![]() ,且
,且![]() 是线段
是线段![]() 的中点,求
的中点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com