【答案】
分析:A、如图,利用 EC∥DB,AB:AC=AD:AE=2r
1:2r
2,证出结论.
B、设向量
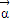
=

,由 A
2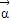
=
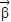
,利用矩阵的运算法则,用待定系数法可得x 和 y 的值,从而求得向量
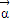
.
C、把椭圆的参数方程化为普通方程,求出右焦点的坐标,把直线参数方程化为普通方程,求出斜率,用点斜式
求得所求直线的方程.
D、原不等式可化为
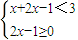
,或
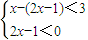
,分别解出这两个不等式组的解集,
再把解集取并集.
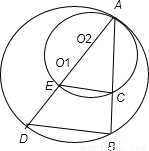
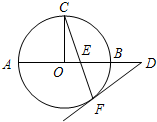
解答:解:A、如图:连接AO
1并延长,交两圆于D,E,则O
2在AD上,根据直径对的圆周角等于90°可得,∠ACE=∠ABD=90°,
∴EC∥DB,∴AB:AC=AD:AE=2r
1:2r
2=r
1:r
2 为定值.
B、A
2=


=

,设向量
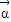
=

,由 A
2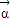
=
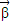
可得


=

,∴
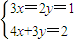
,解得 x=-1,y=2,
∴向量
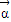
=

.
C、椭圆
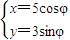
(φ为参数)的普通方程为
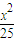
+
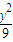
=1,右焦点为(4,0),
直线
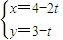
(t为参数) 即 x-2 y+2=0,斜率等于

,故所求的直线方程为
y-0=

(x-4),即 x-2 y-4=0.
D、原不等式可化为
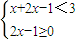
,或
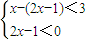
,
解得

≤x<

,或-2<x<

,故不等式的解集为 {x|-2<x<

}.
点评:本题考查圆与圆的位置关系,参数方程与普通方程的互化,矩阵的运算法则,绝对值不等式的解法.

 ,向量
,向量 .求向量
.求向量 ,使得A2
,使得A2 =
=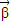 .
.  (φ为参数)的右焦点,且与直线
(φ为参数)的右焦点,且与直线 (t为参数)平行的直线的普通方程.
(t为参数)平行的直线的普通方程.
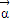 =
= ,由 A2
,由 A2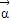 =
=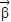 ,利用矩阵的运算法则,用待定系数法可得x 和 y 的值,从而求得向量
,利用矩阵的运算法则,用待定系数法可得x 和 y 的值,从而求得向量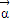 .
.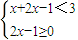 ,或
,或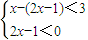 ,分别解出这两个不等式组的解集,
,分别解出这两个不等式组的解集,

 =
= ,设向量
,设向量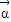 =
= ,由 A2
,由 A2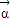 =
=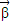 可得
可得
 =
= ,∴
,∴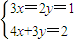 ,解得 x=-1,y=2,
,解得 x=-1,y=2,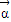 =
= .
.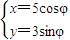 (φ为参数)的普通方程为
(φ为参数)的普通方程为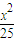 +
+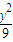 =1,右焦点为(4,0),
=1,右焦点为(4,0),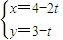 (t为参数) 即 x-2 y+2=0,斜率等于
(t为参数) 即 x-2 y+2=0,斜率等于 ,故所求的直线方程为
,故所求的直线方程为 (x-4),即 x-2 y-4=0.
(x-4),即 x-2 y-4=0.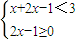 ,或
,或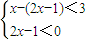 ,
, ≤x<
≤x< ,或-2<x<
,或-2<x< ,故不等式的解集为 {x|-2<x<
,故不等式的解集为 {x|-2<x< }.
}.

 A(选修4-1:几何证明选讲)
A(选修4-1:几何证明选讲) 选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤.
选做题:在A、B、C、D四小题中只能选做2题,每小题10分,共20分.解答应写出文字说明、证明过程或演算步骤. A)选修4-1:几何证明选讲
A)选修4-1:几何证明选讲 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分. 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)