
【题目】设函数f(x)=x﹣a(x+1)ln(x+1),(x>﹣1,a≥0)
(Ⅰ)求f(x)的单调区间;
(Ⅱ)当a=1时,若方程f(x)=t在 ![]() 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;
(Ⅲ)证明:当m>n>0时,(1+m)n<(1+n)m .
【答案】解:(Ⅰ)f′(x)=1﹣aln(x+1)﹣a
①a=0时,f′(x)>0∴f(x)在(﹣1,+∞)上是增函数
②当a>0时,f(x)在 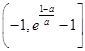 上递增,在
上递增,在 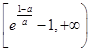 单调递减
单调递减
(Ⅱ)由(Ⅰ)知,f(x)在 ![]() 上单调递增,在[0,1]上单调递减
上单调递增,在[0,1]上单调递减
又 ![]()
∴ ![]()
∴当 ![]() 时,方程f(x)=t有两解
时,方程f(x)=t有两解
(Ⅲ)要证:(1+m)n<(1+n)m只需证nln(1+m)<mln(1+n),
只需证: ![]()
设 ![]() ,则
,则 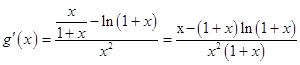
由(Ⅰ)知x﹣(1+x)ln(1+x),在(0,+∞)单调递减
∴x﹣(1+x)ln(1+x)<0,即g(x)是减函数,而m>n
∴g(m)<g(n),故原不等式成立.
【解析】(Ⅰ)求导数,再利用导数大于0,求函数的单调区间;(Ⅱ)由(Ⅰ)知,f(x)在 ![]() 上单调递增,在[0,1]上单调递减可得解(Ⅲ)根据要证明的结论,利用分析法来证明本题,从结论入手,要证结论只要证明后面这个式子成立,两边取对数,构造函数,问题转化为只要证明函数在一个范围上成立,利用导数证明函数的性质.
上单调递增,在[0,1]上单调递减可得解(Ⅲ)根据要证明的结论,利用分析法来证明本题,从结论入手,要证结论只要证明后面这个式子成立,两边取对数,构造函数,问题转化为只要证明函数在一个范围上成立,利用导数证明函数的性质.
【考点精析】本题主要考查了利用导数研究函数的单调性和不等式的证明的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等才能正确解答此题.
在这个区间单调递减;不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等才能正确解答此题.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】一个盒子中装有4个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从盒子中不放回随机抽取两个球,求取出的球的编号之和不大于4的概率;
(2)先从盒子中随机取一个球,该球的编号为![]() ,将球放回盒子中,然后再从盒子中随机取一个球,该球的编号为
,将球放回盒子中,然后再从盒子中随机取一个球,该球的编号为![]() ,求
,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
注:年份代码1﹣7分别对应年份2008﹣2014.
(1)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以证明;
(2)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据: ![]() =9.32,
=9.32, ![]() =40.17,
=40.17, ![]() =0.55,
=0.55, ![]() ≈2.646.
≈2.646.
参考公式:  ,
,
回归方程 ![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数是( )
①命题“x0∈R,x02+1>3x0”的否定是“x∈R,x2+1≤3x”;
②“函数f(x)=cos2ax﹣sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
③x2+2x≥ax在x∈[1,2]上恒成立(x2+2x)min≥(ax)max在x∈[1,2]上恒成立;
④“平面向量 ![]() 与
与 ![]() 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“ ![]()
![]() <0”.
<0”.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=|x﹣1|﹣2|x+1|的最大值为m.
(Ⅰ)求m;
(Ⅱ)若a,b,c∈(0,+∞),a2+2b2+c2=m,求ab+bc的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点 P 与定点![]() 的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.
的距离和它到定直线 x 4 的距离的比是1: 2 ,记动点 P 的轨迹为曲线 E.
(1)求曲线 E 的方程;
(2)设 A 是曲线 E 上的一个点,直线 AF 交曲线 E 于另一点 B,以 AB 为边作一个平行四边形,顶点 A、B、C、D 都在轨迹 E 上,判断平行四边形 ABCD 能否为菱形,并说明理由;
(3)当平行四边形 ABCD 的面积取到最大值时,判断它的形状,并求出其最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,直线l经过点P(﹣1,0),其倾斜角为α,在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为ρ2﹣6ρcosθ+1=0. (Ⅰ)若直线l与曲线C有公共点,求α的取值范围;
(Ⅱ)设M(x,y)为曲线C上任意一点,求x+y的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com