【题目】若 
的平均数为3，标准差为4，且 
， 
，则新数据 
的平均数和标准差分别为（ ）
A.-9 12
B.-9 36
C.3 36
D.-3 12
【答案】D
【解析】由平均数和标准差的性质可知，若 
的平均数为 
，标准差为 
，
则： 
的平均数为 
，标准差为 
，
据此结合题意可得：
的平均数为： 
，标准差分别为 
， 所以答案是：D.
【考点精析】根据题目的已知条件，利用平均数、中位数、众数和极差、方差与标准差的相关知识可以得到问题的答案，需要掌握⑴平均数、众数和中位数都是描述一组数据集中趋势的量；⑵平均数、众数和中位数都有单位；⑶平均数反映一组数据的平均水平，与这组数据中的每个数都有关系，所以最为重要，应用最广；⑷中位数不受个别偏大或偏小数据的影响；⑸众数与各组数据出现的频数有关，不受个别数据的影响，有时是我们最为关心的数据；标准差和方差越大，数据的离散程度越大；标准差和方程为0时，样本各数据全相等，数据没有离散性；方差与原始数据单位不同，解决实际问题时，多采用标准差．
特高级教师点拨系列答案科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝2x－ 
的定义域为(0，1](a为实数).
（1）当a＝1时，求函数y＝f(x)的值域；
（2）求函数y＝f(x)在区间(0，1]上的最大值及最小值，并求出当函数f(x)取得最值时x的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知 
为坐标原点， 
， 
是椭圆 
上的点，且 
，设动点 
满足 
．
（Ⅰ）求动点 的轨迹 
的方程；
（Ⅱ）若直线 
与曲线 交于 
两点，求三角形 
面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数 
，给出以下四个命题：
① 
，有 
；
② 
且 
，有 
；
③ 
，有 
；
④ ， 
.
其中所有真命题的序号是（ ）
A.①②
B.③④
C.①②③
D.①②③④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在四棱锥
中，底面
为平行四边形， 
， 
， 
， 
点在底面
内的射影
在线段
上，且
， 
， 
为
的中点， 
在线段
上，且
．
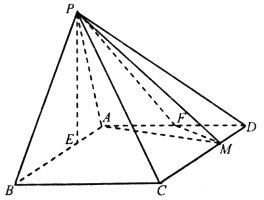
（Ⅰ）当
时，证明：平面
平面
；
（Ⅱ）当平面
与平面
所成的二面角的正弦值为
时，求四棱锥
的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上.
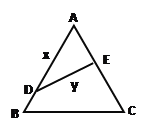
（1）设AD＝x（x≥1），ED＝y，求用x表示y的函数关系式；
（2）如果DE是灌溉水管，为节约成本，希望它最短，DE的位置应在哪里？如果DE是参观线路，则希望它最长，DE的位置又应在哪里？请予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
