练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系中，已知两定点，，动点满足.

    （1）求动点的轨迹的方程；

    （2）轨迹上有两点，，它们关于直线：对称，且满足，求的面积.

    【答案】（1）动点的轨迹是圆，其方程为（2）

    【解析】

    （1）设动点的坐标为表示出化简可得.
    （2）根据对称，由垂径定理可得圆心在直线：上，即可求出直线的方程，易知垂直于直线，且.设的中点为，则，计算可得，，的值，即可求出的面积.

    （1）设动点的坐标为，则.

    整理得，故动点的轨迹是圆，且方程为.

    （2）由（1）知动点的轨迹是圆心为，半径的圆，圆上两点，关于直线对称，由垂径定理可得圆心在直线：上，代入并求得，故直线的方程为.

    易知垂直于直线，且.

    设的中点为，则

    ，又，.

    ∴，，∴，.

    易知，故到的距离等于，∴.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】每个国家身高正常的标准是不一样的，不同年龄、不同种族、不同地区身高都是有差异的，我们国家会定期进行0～18岁孩子身高体重全国性调查，然后根据这个调查结果制定出相应的各个年龄段的身高标准.一般测量出一个孩子的身高，对照一下身高体重表，如果在平均值标准差以内的就说明你的孩子身高是正常的，否则说明你的孩子可能身高偏矮或偏高了.根据科学研究0～18岁的孩子的身高服从正态分布.在某城市随机抽取100名18岁男大学生得到其身高（）的数据.

    （1）记表示随机抽取的100名18岁男大学生身高的数据在之内的人数，求及的数学期望.

    （2）若18岁男大学生身高的数据在之内，则说明孩子的身高是正常的.

    （i）请用统计学的知识分析该市18岁男大学生身高的情况；

    （ii）下面是抽取的100名18岁男大学生中20名大学生身高（）的数据：

    1.65

    1.62

    1.74

    1.82

    1.68

    1.72

    1.75

    1.66

    1.73

    1.67

    1.86

    1.81

    1.74

    1.69

    1.76

    1.77

    1.69

    1.78

    1.63

    1.68

    经计算得，，其中为抽取的第个学生的身高，.用样本平均数作为的估计值，用样本标准差作为的估计，剔除之外的数据，用剩下的数据估计和的值.（精确到0.01）

    附：若随机变量服从正态分布，则，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个命题中真命题是　　

    A. 同垂直于一直线的两条直线互相平行

    B. 底面各边相等，侧面都是矩形的四棱柱是正四棱柱

    C. 过空间任一点与两条异面直线都垂直的直线有且只有一条

    D. 过球面上任意两点的大圆有且只有一个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥P-ABC中，已知，顶点P在平面ABC上的射影为的外接圆圆心.

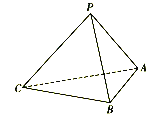
    （1）证明：平面平面ABC；

    （2）若点M在棱PA上，，且二面角P-BC-M的余弦值为，试求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】绿水青山就是金山银山.近年来，祖国各地依托本地自然资源，打造旅游产业，旅游业正蓬勃发展.景区与游客都应树立尊重自然、顺应自然、保护自然的生态文明理念，合力使旅游市场走上规范有序且可持续的发展轨道.某景区有一个自愿消费的项目：在参观某特色景点入口处会为每位游客拍一张与景点的合影，参观后，在景点出口处会将刚拍下的照片打印出来，游客可自由选择是否带走照片，若带走照片则需支付20元，没有被带走的照片会收集起来统一销毁.该项目运营一段吋间后，统计出平均只有三成的游客会选择带走照片，为改善运营状况，该项目组就照片收费与游客消费意愿关系作了市场调研，发现收费与消费意愿有较强的线性相关性，并统计出在原有的基础上，价格每下调1元，游客选择带走照片的可能性平均增加0.05，假设平均每天约有5000人参观该特色景点，每张照片的综合成本为5元，假设每个游客是否购买照片相互独立.

    （1）若调整为支付10元就可带走照片，该项目每天的平均利润比调整前多还是少？

    （2）要使每天的平均利润达到最大值，应如何定价？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设抛物线C:与直线交于A、B两点.

    （1）当取得最小值为时，求的值.

    （2）在（1）的条件下，过点作两条直线PM、PN分别交抛物线C于M、N（M、N不同于点P）两点，且的平分线与轴平行，求证：直线MN的斜率为定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,在四棱锥中，平面平面，，，，，点在棱上，且.

    （Ⅰ）求证：；

    （Ⅱ）是否存在实数，使得二面角的余弦值为？若存在，求出实数的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2011年国际数学协会正式宣布，将每年的3月14日设为国际数学节，来源于中国古代数学家祖冲之的圆周率。公元263年，中国数学家刘徽用“割圆术”计算圆周率，计算到圆内接3072边形的面积，得到的圆周率是.公元480年左右，南北朝时期的数学家祖冲之进一步得出精确到小数点后7位的结果，给出不足近似值3.1415926和过剩近似值3.1415927，还得到两个近似分数值，密率和约率。大约在公元530年，印度数学大师阿耶波多算出圆周率约为（）.在这4个圆周率的近似值中，最接近真实值的是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的右焦点为，且点在椭圆C上.

    （1）求椭圆C的标准方程；

    （2）过椭圆上异于其顶点的任意一点Q作圆的两条切线，切点分别为不在坐标轴上），若直线在x轴，y轴上的截距分别为，证明：为定值；

    （3）若是椭圆上不同两点，轴，圆E过，且椭圆上任意一点都不在圆E内，则称圆E为该椭圆的一个内切圆，试问：椭圆是否存在过焦点F的内切圆？若存在，求出圆心E的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案