
【题目】(导学号:05856262)
如图所示,在斜三棱柱ABC-A1B1C1中,AB=BC=1,AA1=2,D是AC的中点,AB⊥平面B1C1CB,∠BCC1=60°.
(Ⅰ)求证:AC⊥平面BDC1;
(Ⅱ)E是线段CC1上的动点,判断点E到平面AA1B1B的距离是否为定值,若是,求出此定值;否则,说明理由.

【答案】(1)见解析;(2)定值为![]()
【解析】试题分析:(1)利用余弦定理易证C1B⊥BC,又平面ABC⊥平面BCC1B1所以C1B⊥平面ABC进而易得AC⊥平面BDC1(2)CC1∥平面A1B1BA,所以点E到平面A1B1BA的距离与E的位置无关,为一定值.利用等积法构建所求量的方程,解之即可.
试题解析:
(Ⅰ)在△BCC1中,BC=BC2+CC-2BC×CC1×cos∠BCC1=1+4-2×1×2×![]() =3,
=3,
∵CC=BC2+BC,∴C1B⊥BC.∵AB⊥平面BCC1B1,∴平面ABC⊥平面BCC1B1,
∴C1B⊥平面ABC,则平面BC1D⊥平面ABC.
∵AB=BC,D是AC的中点,∴AC⊥BD,∴AC⊥平面BDC1.
(Ⅱ)∵CC1∥BB1,∴CC1∥平面A1B1BA,所以点E到平面A1B1BA的距离与E的位置无关,为一定值.
∵A1B1∥AB,∴A1B1⊥平面B1C1CB.
设点E到平面AA1BB1的距离为h,则VE-A1B1B=VA1-B1BE.
∵S△A1B1B=![]() ×A1B1×BB1=
×A1B1×BB1=![]() ×1×2=1,
×1×2=1,
S△BB1E=![]() SBCC1B1=S△BC1C=
SBCC1B1=S△BC1C=![]() BC1×BC=
BC1×BC=![]() ,
,
∴![]() S△A1B1B×h=
S△A1B1B×h=![]() S△BB1E×A1B1,即h=
S△BB1E×A1B1,即h=![]() ,也即点E到平面AA1B1B的距离为
,也即点E到平面AA1B1B的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知各项都为正数的数列{an}满足a1=1, ![]() =2an+1(an+1)-an.
=2an+1(an+1)-an.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=![]() ,求数列{an·bn}的前n项和Tn.
,求数列{an·bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·黄冈质检)如图,在棱长均为2的正四棱锥P-ABCD中,点E为PC的中点,则下列命题正确的是( )
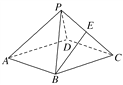
A. BE∥平面PAD,且BE到平面PAD的距离为![]()
B. BE∥平面PAD,且BE到平面PAD的距离为![]()
C. BE与平面PAD不平行,且BE与平面PAD所成的角大于30°
D. BE与平面PAD不平行,且BE与平面PAD所成的角小于30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
(Ⅰ)求C;(Ⅱ)若c=![]() ,△ABC的面积为
,△ABC的面积为![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·河西五市二联)下列说法正确的是( )
A. 命题“x∈R,ex>0”的否定是“x∈R,ex>0”
B. 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题
C. “x2+2x≥ax在x∈[1,2]上恒成立”“(x2+2x)min≥(ax)min在x∈[1,2]上恒成立”
D. 命题“若a=-1,则函数f(x)=ax2+2x-1只有一个零点”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是递增的等比数列,满足
是递增的等比数列,满足![]() ,且
,且![]() 是
是![]() 、
、![]() 的等差中项,数列
的等差中项,数列![]() 满足
满足![]() ,其前
,其前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)数列![]() 的前
的前![]() 项和为
项和为![]() ,若不等式
,若不等式![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856307)(12分)
某老师为了分析学生的学习情况,随机抽取了班上20名学生某次期末考试的成绩(满分为150分)进行分析,统计如下:
男生:133 131 130 126 123 120 116 109 107 105
女生:136 127 125 123 119 118 117 114 113 108
(Ⅰ)计算男、女生成绩的平均值并分析比较男、女生成绩的分散程度;
(Ⅱ)现从分数在120分以下的女同学中随机抽取2位,求这两位同学分数之差的绝对值小于10的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com