
分析 以AB所在直线为x轴,AB中点为原点建立直角坐标系,设AB=r,点C的坐标为(x,y),可得G($\frac{x}{3}$,$\frac{y}{3}$).根据AG⊥BG建立x、y的关系式,化简整理得x2+y2=9r2,得到点C在以原点为圆心,半径为3r的圆上运动(x轴上两点除外).可得当C点在y轴时y的值达到最大值,此时三角形面积最大,由此结合三角形面积公式即可得解.
解答 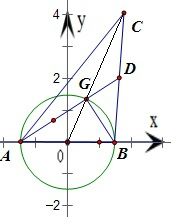 解:设AB中点为O,连接AO,可得重心G在CO上且$\overrightarrow{OG}$=$\frac{1}{3}$$\overrightarrow{OC}$,
解:设AB中点为O,连接AO,可得重心G在CO上且$\overrightarrow{OG}$=$\frac{1}{3}$$\overrightarrow{OC}$,
以AB所在直线为x轴,AB中点为原点建立如图所示直角坐标系,
设AB=2r(r>0),则A(-r,0),B(r,0),
设C(x,y),可得G($\frac{x}{3}$,$\frac{y}{3}$)
∵AG⊥BG,
∴点G在以AB为直径的圆上运动(A、B两点除外)
由此可得($\frac{x}{3}$)2+($\frac{y}{3}$)2=r2,整理得x2+y2=9r2,
因此,点C在以原点为圆心,半径为3r的圆上运动(x轴上两点除外),
可得,当x=0时,y取得最大值3r,
∴此时,tan$\frac{C}{2}$=$\frac{1}{3}$,AC=BC=2,
∵r2+(3r)2=2,解得:r=$\frac{\sqrt{10}}{5}$,
∴此时,S△ABC=$\frac{1}{2}×2r×3r$=$\frac{6}{5}$.
故答案为:$\frac{6}{5}$.
点评 本题给出三角形的重心G对A、B的张角为直角,求三角形面积的最大值,着重考查了三角形重心的性质、圆的标准方程和三角恒等变换等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | “|am|<|bm|”是“|a|<|b|”的充分不必要条件 | |
| B. | 命题“?x∈R,ax+b≤0”的否定是“?x0∈R,ax0+b>0” | |
| C. | 若¬(p∧q)为真命题,则p,q均为假命题 | |
| D. | 命题“若p,则¬q”为真命题,则“若q,则¬p”也为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-1,-\frac{1}{4})$ | B. | $(-1,-\frac{1}{4}]$ | C. | (-1,+∞) | D. | $(-∞,-\frac{1}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
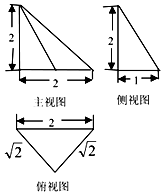
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
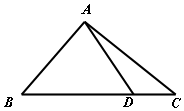 如图,已知D是△ABC边BC上一点.
如图,已知D是△ABC边BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | 9 | C. | $\frac{{9\sqrt{3}}}{2}$ | D. | $\frac{{9\sqrt{3}}}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com