
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若数列![]() 的前
的前![]() 项成公差不为0的等差数列,求
项成公差不为0的等差数列,求![]() 的最大值;
的最大值;
(3)若![]() ,是否存在
,是否存在![]() ,使
,使![]() 为等比数列?若存在,求出所有符合题意的
为等比数列?若存在,求出所有符合题意的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)4;(3)存在;
;(2)4;(3)存在;![]() .
.
【解析】
(1)记![]() 为
为![]() 式.当
式.当![]() 时,
时,![]() 式为
式为![]() ,令
,令![]() 得,
得,![]() ,转化求解即可.
,转化求解即可.
(2)设公差为![]() ,若
,若![]() ,则
,则![]() ,
,![]() .在
.在![]() 式中,令
式中,令![]() 得,
得,![]() ,推出
,推出![]() ,若
,若![]() ,推出
,推出![]() ,求解可得
,求解可得![]() ,
,![]() .所以
.所以![]() 符合题意.验证
符合题意.验证![]() ,是否成立,推出结果.
,是否成立,推出结果.
(3)假设存在![]() ,使
,使![]() 为等比数列,推出
为等比数列,推出![]() ,结合
,结合![]() ,推出
,推出![]() ,得到数列
,得到数列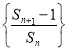 为常数列,转化求解证明即可.
为常数列,转化求解证明即可.
解:记![]() 为
为![]() 式.
式.
(1)当![]() 时,
时,![]() 式为
式为![]() ,
,
令![]() 得,
得,![]() ,即
,即![]() ,
,
由已知![]() ,
,![]() ,解得
,解得![]() .
.
(2)因为前![]() 项成等差数列,设公差为
项成等差数列,设公差为![]() ,则
,则![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,
,![]() .
.
在![]() 式中,令
式中,令![]() 得,
得,![]() ,所以
,所以![]() ,
,
化简得![]() ,①
,①
若![]() ,则
,则![]() ,
,
在![]() 式中,令
式中,令![]() 得,
得,![]() ,所以
,所以![]() ,
,
化简得![]() ,②
,②
②![]() ①得,
①得,![]() ,因为公差不为0,所以
,因为公差不为0,所以![]() ,
,
所以![]() ,代入①得,
,代入①得,![]() ,所以
,所以![]() ,
,![]() .
.
所以![]() 符合题意.
符合题意.
若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
在![]() 式中,令
式中,令![]() 得,
得,![]() ,
,
![]() ,所以
,所以![]() ,所以
,所以![]() 的最大值为4.
的最大值为4.
(3)假设存在![]() ,使
,使![]() 为等比数列,
为等比数列,
设前3项分别为1,![]() ,
,![]() ,则
,则![]() ,
,
![]() 式中,令
式中,令![]() 得,
得,![]() ,化简得
,化简得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
此时![]() 式为
式为![]() ,即
,即![]() ,
,
由![]() ,
,![]() ,得
,得![]() ,由
,由![]() ,
,![]() 得
得![]() ,
,![]() ,
,
依此类推,![]() ,所以
,所以![]() 等价于
等价于![]() ,
,
所以数列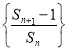 为常数列,
为常数列,
所以![]() ,
,
于是![]() 时,
时,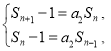 两式相减得
两式相减得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() (非零常数),
(非零常数),
所以存在![]() ,使
,使![]() 为等比数列.
为等比数列.


科目:高中数学 来源: 题型:
【题目】已知直线L的参数方程为:![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(Ⅰ)求曲线C的参数方程;
(Ⅱ)当![]() 时,求直线l与曲线C交点的极坐标.
时,求直线l与曲线C交点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人![]() 次数学考试的成绩,统计结果如下表:
次数学考试的成绩,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩(分) |
|
|
|
|
|
乙的成绩(分) |
|
|
|
|
|
(1)若从甲、乙两人中选出一人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若答对,则可参加复赛,否则被淘汰.
道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若至少答对其中
道,若至少答对其中![]() 道,则可参加复赛,否则被润汰.
道,则可参加复赛,否则被润汰.
已知学生甲、乙都只会![]() 道备选题中的
道备选题中的![]() 道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新冠肺炎疫情这只“黑天鹅”的出现,给经济运行带来明显影响,住宿餐饮、文体娱乐、交通运输、旅游等行业受疫情影响严重.随着复工复产的有序推动,我市某西餐厅推出线上促销活动:
A套餐(在下列食品中6选3)
西式面点:蔓越莓核桃包、南瓜芝土包、黑列巴、全麦吐司;
中式面点:豆包、桂花糕
B套餐:酱牛肉、老味烧鸡熟食类组合.
复工复产后某一周两种套餐的日销售量(单位:份)如下:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | |
A套餐 | 11 | 12 | 14 | 18 | 22 | 19 | 23 |
B套餐 | 6 | 13 | 15 | 15 | 37 | 20 | 41 |
(1)根据该西餐厅上面一周A、B两种套餐的销售情况,结合两种套餐的平均销售量和方差,评价两种套餐的销售情况(不需要计算,只给出结论即可);
(2)如果该西餐厅每种套餐每日销量少于20份表示业绩“一般”,销量大于等于20份表示业绩“优秀”,求该西餐厅在这一周内B套餐连续两天中至少有一天销量业绩为“优秀”的概率;
(3)某顾客购买一份A套餐,求她所选的面点中所含中式面点个数X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市9年前分别同时开始建设物流城和湿地公园,物流城3年建设完成,建成后若年投入x亿元,该年产生的经济净效益为![]() 亿元;湿地公园4年建设完成,建成后的5年每年投入见散点图.公园建成后若年投入x亿元,该年产生的经济净效益为
亿元;湿地公园4年建设完成,建成后的5年每年投入见散点图.公园建成后若年投入x亿元,该年产生的经济净效益为![]() 亿元.
亿元.

(1)对湿地公园,请在![]() 中选择一个合适模型,求投入额x与投入年份n的回归方程;
中选择一个合适模型,求投入额x与投入年份n的回归方程;
(2)从建设开始的第10年,若对物流城投入0.25亿元,预测这一年物流城和湿地公园哪个产生的年经济净效益高?请说明理由.
参考数据及公式:![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() ,回归方程中的
,回归方程中的![]() ;回归方程
;回归方程![]() 斜率与截距
斜率与截距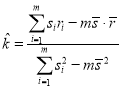 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一条线段,且
上的一条线段,且![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是棱
是棱![]() 上的动点,则
上的动点,则
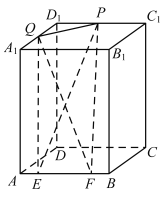
①四面体![]() 的体积为定值
的体积为定值
②直线![]() 到平面
到平面![]() 的距离为定值
的距离为定值
③点![]() 到直线
到直线![]() 的距离为定值
的距离为定值
④直线![]() 与平面
与平面![]() 所成的角为定值
所成的角为定值
其中正确结论的编号是( )
A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产了一批零件,从中随机抽取100个作为样本,测出它们的长度(单位:厘米),按数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 5组,得到如图所示的频率分布直方图.以这100个零件的长度在各组的频率代替整批零件长度在该组的概率.
5组,得到如图所示的频率分布直方图.以这100个零件的长度在各组的频率代替整批零件长度在该组的概率.
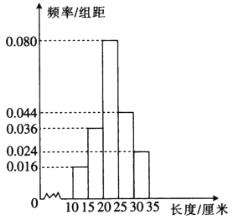
(1)估计该工厂生产的这批零件长度的平均值(同一组中的每个数据用该组区间的中点值代替);
(2)规定零件长度在区间![]() 内的零件为优等品,从这批零件中随机抽取3个,记抽到优等品的个数为X,求X的分布列和数学期望.
内的零件为优等品,从这批零件中随机抽取3个,记抽到优等品的个数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com