
【题目】已知函数![]() (
(![]() ,且
,且![]() 为常数).
为常数).
(1)若函数![]() 的图象在
的图象在![]() 处的切线的斜率为
处的切线的斜率为![]() (
(![]() 为自然对数的底数),求
为自然对数的底数),求![]() 的值;
的值;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(3)已知![]() ,且
,且![]() .求证:
.求证:![]() .
.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)根据导数几何意义知![]() ,由此构造方程求得结果;
,由此构造方程求得结果;
(2)将问题转化为![]() 且
且![]() 恒成立的问题,令
恒成立的问题,令![]() ,分别在
,分别在![]() 、
、![]() 和
和![]() 或
或![]() 时,结合函数单调性确定最小值,令
时,结合函数单调性确定最小值,令![]() ,从而求得
,从而求得![]() 的取值范围;
的取值范围;
(3)根据(2)的结论可知![]() 在
在![]() 上单调递增,分类讨论可确定
上单调递增,分类讨论可确定![]() ,将不等关系代入所求不等式左侧,结合对数运算可整理得到结果.
,将不等关系代入所求不等式左侧,结合对数运算可整理得到结果.
(1)由题意得: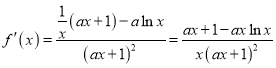
![]()
![]() 的图象在
的图象在![]() 处的切线的斜率为
处的切线的斜率为![]() ,
,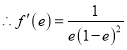 ,
,
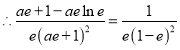 ,解得:
,解得:![]() ,
,
![]() ,
,![]() 或
或![]() ;
;
(2)![]() 函数
函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 对于任意的
对于任意的![]() ,都有
,都有![]() 恒成立
恒成立
即![]() 且
且![]() ,
,
当![]() ,
,![]() 恒成立,满足题意;
恒成立,满足题意;
当![]() 时,由
时,由![]() 得:
得:![]() ,即
,即![]() 或
或![]() 或
或![]() ,
,
令![]() ,则
,则![]() ,
,
①当![]() 且
且![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
要使得![]() 恒成立,即要求
恒成立,即要求![]() ,
,
即![]() ,解得:
,解得:![]() ,
,![]() 满足题意;
满足题意;
②当![]() 或
或![]() ,且
,且![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
要使得![]() 恒成立,即要求
恒成立,即要求![]() ,
,
即![]() ,解得:
,解得:![]() ;
;
![]() 或
或![]()
综上所述:![]() 的取值范围是
的取值范围是![]() ;
;
(3)由(2)可知:当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,此时
上单调递增,此时![]() ,
,
当![]() 时,
时,![]() ,而
,而![]() ,
,
![]() ,即
,即![]() ,
,
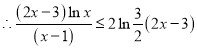 ,
,
当![]() 时,
时,![]() ,而
,而![]() ,
,
![]() ,即
,即![]() ,
,
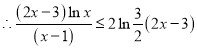
综上,对于任意![]() ,都有
,都有![]() ,
,

![]() ,结论得证.
,结论得证.


科目:高中数学 来源: 题型:
【题目】如图,![]() 是边长为2的正方形,
是边长为2的正方形,![]() 平面
平面![]() ,且
,且![]() .
.
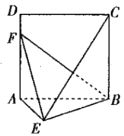
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)线段![]() 上是否存在一点
上是否存在一点![]() ,使二而角
,使二而角![]() 等于45°?若存在,请找出点
等于45°?若存在,请找出点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 与两焦点构成的三角形的周长为6,离心率为
与两焦点构成的三角形的周长为6,离心率为![]() ,
,

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,问在
两点,问在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?证明你的结论.
为定值?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是一个单调递增的等比数列,
是一个单调递增的等比数列,![]() 是一个等差数列,
是一个等差数列,![]() 是
是![]() 的前
的前![]() 项和,其中
项和,其中![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)若![]() ,
,![]() ,
,![]() 既成等比数列,又成等差数列.
既成等比数列,又成等差数列.
(i)求![]() 的通项公式;
的通项公式;
(ii)对于数列![]() ,若
,若![]() 且
且![]() ,或
,或![]() 且
且![]() ,则
,则![]() 为数列
为数列![]() 的转折点,求
的转折点,求![]() 的转折点个数.
的转折点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早晩读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成如表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为![]() ,则优秀分数线应定为多少分?
,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有![]() 的把握认为赞成与否的态度与成绩是否优秀有关系.
的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: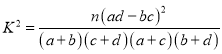 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
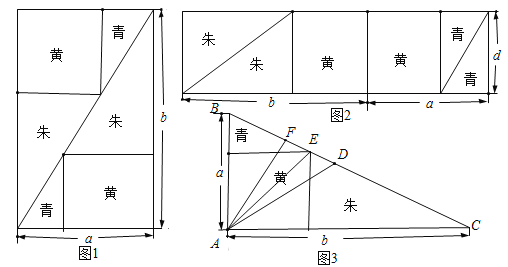
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得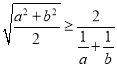 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com