
已知函数f(x)=ln x+ax(a∈R).
(1)求f(x)的单调区间;
(2)设g(x)=x2-4x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
(1) f(x)的单调递增区间为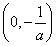 ,单调递减区间为
,单调递减区间为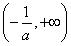 (2)
(2)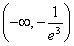
【解析】(1)f′(x)=a+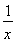 =
=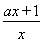 (x>0).
(x>0).
①当a≥0时,由于x>0,故ax+1>0,
f′(x)>0,
所以f(x)的单调递增区间为(0,+∞).
②当a<0时,由f′(x)=0,得x=-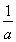 .
.
在区间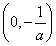 上,f′(x)>0,在区间
上,f′(x)>0,在区间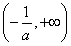 上,f′(x)<0,所以函数f(x)的单调递增区间为
上,f′(x)<0,所以函数f(x)的单调递增区间为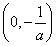 ,单调递减区间为
,单调递减区间为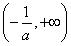 .
.
(2)由题意得f(x)max<g(x)max,而g(x)max=2,
由(1)知,当a≥0时,f(x)在(0,+∞)上单调递增,值域为R,故不符合题意.
当a<0时,f(x)在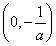 上单调递增,在
上单调递增,在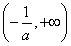 上单调递减,
上单调递减,
故f(x)的极大值即为最大值,f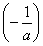 =-1+ln
=-1+ln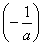 =-1-ln(-a),所以2>-1-ln(-a),解得a<-
=-1-ln(-a),所以2>-1-ln(-a),解得a<-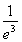 .
.
故a的取值范围为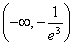 .
.


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:填空题
若数列{an}的前n项和Sn=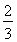 an+
an+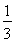 ,则{an}的通项公式是an=________.
,则{an}的通项公式是an=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
已知i为虚数单位,复数z=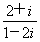 ,则|z|+
,则|z|+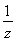 =( )
=( )
A.i B.1-I C.1+i D.-i
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:填空题
函数y=sin(ωx+φ) (ω>0,0<φ<π)的最小正周期为π,且函数图象关于点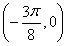 对称,则函数的解析式为________.
对称,则函数的解析式为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:选择题
已知sin α-cos α=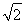 ,α∈(0,π),则tan α=( )
,α∈(0,π),则tan α=( )
A.-1 B.-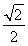 C.
C.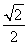 D.1
D.1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第4课时练习卷(解析版) 题型:解答题
已知函数f(x)=|x-a|.
(1)若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2)在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:填空题
已知数列1,a1,a2,9是等差数列,数列1,b1,b2,b3,9是等比数列,则 的值为________.
的值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com