
ЁОЬтФПЁПФГЩЬГЁдЄМЦШЋФъЗжХњЙКШыУПЬЈМлжЕ2000дЊЕФЕчЪгЛњЙВ3600ЬЈЃЌУПХњЙКШыЕФЬЈЪ§ЯрЭЌЃЌЧвУПХњОљаыИЖдЫЗб400дЊЃЌДЂДцЙКШыЕФЕчЪгЛњШЋФъЫљИЖБЃЙмЗбгыУПХњЙКШыЕчЪгЛњЕФзмМлжЕЃЈВЛКЌдЫЗбЃЉГЩе§БШЃЎШєУПХњЙКШы400ЬЈЃЌдђШЋФъашгУШЅдЫЗбКЭБЃЙмЗб43600дЊЃЎЯждкШЋФъжЛга24000дЊПЩгУгкжЇИЖдЫЗбКЭБЃЙмЗбЃЌЧыЮЪФмЗёЧЁЕБАВХХУПХњНјЛѕЕФЪ§СПЃЌЪЙет24000дЊЕФзЪН№ЙЛгУЃПаДГіФуЕФНсТлЃЌВЂЫЕУїРэгЩЃЎ
ЁОД№АИЁПНтЃКЩшШЋФъашгУШЅЕФдЫЗбКЭБЃЙмЗбЕФзмЗбгУЮЊyдЊЃЌЬтжаЕФБШР§ЯЕЪ§ЩшЮЊkЃЌУПХњЙКШыxЬЈЃЌдђЙВашЗж ![]() ХњЃЌ
ХњЃЌ
УПХњЗбгУ2000xдЊЃЎ
гЩЬтвтжЊy= ![]() ЁС400+2000kxЃЌ
ЁС400+2000kxЃЌ
ЕБx=400ЪБЃЌy=43600ЃЌ
НтЕУk= ![]()
Ёрy= ![]() ЁС400+100xЁн2
ЁС400+100xЁн2 ![]() =24000ЃЈдЊЃЉ
=24000ЃЈдЊЃЉ
ЕБЧвНіЕБ ![]() ЁС400=100xЃЌМДx=120ЪБЕШКХГЩСЂЃЎ
ЁС400=100xЃЌМДx=120ЪБЕШКХГЩСЂЃЎ
ДЫЪБx=120ЬЈЃЌШЋФъЙВашвЊзЪН№24000дЊЃЎ
ЙЪжЛашУПХњЙКШы120ЬЈЃЌПЩвдЪЙзЪН№ЙЛгУ
ЁОНтЮіЁПИљОнЬѕМўНЈСЂдЫЗбКЭБЃЙмЗбЕФзмЗбгУyЙигкУПХњЙКШыЬЈЪ§xЕФКЏЪ§НтЮіЪНЃЌШЛКѓРћгУЛљБОВЛЕШЪННјааНтД№ЃЎ
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫЛљБОВЛЕШЪНдкзюжЕЮЪЬтжаЕФгІгУЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮегУЛљБОВЛЕШЪНЧѓзюжЕЪБЃЈЛ§ЖЈКЭзюаЁЃЌКЭЖЈЛ§зюДѓЃЉЃЌвЊзЂвтТњзуШ§ИіЬѕМўЁАвЛе§ЁЂЖўЖЈЁЂШ§ЯрЕШЁБВХФме§ШЗНтД№ДЫЬтЃЎ


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ЪЧЪзЯюЮЊе§Ъ§ЕФЕШВюЪ§СаЃЌa1a2=3ЃЌa2a3=5ЃЎ
ЃЈ1ЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈ2ЃЉЩшbn=ЃЈan+1ЃЉ2 ![]() ЃЌЧѓЪ§Са{bn}ЕФЧАnЯюКЭTn ЃЎ
ЃЌЧѓЪ§Са{bn}ЕФЧАnЯюКЭTn ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]()
![]() .
.
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфЃЛ
ЕФЕЅЕїЧјМфЃЛ
ЃЈ2ЃЉШєЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() гаЪЕЪ§ИљЃЌЧѓЪЕЪ§
гаЪЕЪ§ИљЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОбаЗЂГівЛПюВњЦЗЃЌХњСПЩњВњЧАЯШдкФГГЧЪаЯњЪл30ЬьНјааЪаГЁЕїВщ.ЕїВщНсЙћЗЂЯжЃКШеЯњСП![]() гыЬьЪ§
гыЬьЪ§![]() ЕФЖдгІЙиЯЕЗўДгЭМЂйЫљЪОЕФКЏЪ§ЙиЯЕЃКУПМўВњЦЗЕФЯњЪлРћШѓ
ЕФЖдгІЙиЯЕЗўДгЭМЂйЫљЪОЕФКЏЪ§ЙиЯЕЃКУПМўВњЦЗЕФЯњЪлРћШѓ![]() гыЬьЪ§
гыЬьЪ§![]() ЕФЖдгІЙиЯЕЗўДгЭМЂкЫљЪОЕФКЏЪ§ЙиЯЕ.ЭМЂйгЩХзЮяЯпЕФвЛВПЗжЃЈ
ЕФЖдгІЙиЯЕЗўДгЭМЂкЫљЪОЕФКЏЪ§ЙиЯЕ.ЭМЂйгЩХзЮяЯпЕФвЛВПЗжЃЈ![]() ЮЊХзЮяЯпЖЅЕуЃЉКЭЯпЖЮ
ЮЊХзЮяЯпЖЅЕуЃЉКЭЯпЖЮ![]() зщГЩ.
зщГЩ.
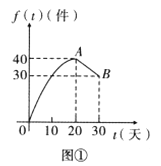
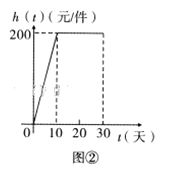
ЃЈЂёЃЉЩшИУВњЦЗЕФШеЯњЪлРћШѓ![]()
![]() ЃЌЗжБ№ЧѓГі
ЃЌЗжБ№ЧѓГі![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЕФНтЮіЪНЃЌ
ЕФНтЮіЪНЃЌ
ЃЈЂђЃЉШєдк30ЬьЕФЯњЪлжаЃЌШеЯњЪлРћШѓжСЩйгавЛЬьГЌЙ§8500дЊЃЌдђПЩвдЭЖШыХњСПЩњВњЃЌИУВњЦЗЪЧЗёПЩвдЭЖШыХњСПЩњВњЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБЯпlЙ§PЃЈ1ЃЌ2ЃЉЃЌЧвAЃЈ2ЃЌ3ЃЉЃЌBЃЈ4ЃЌЉ5ЃЉЕНlЕФОрРыЯрЕШЃЌдђжБЯпlЕФЗНГЬЪЧЃЈ ЃЉ
A.4x+yЉ6=0
B.x+4yЉ6=0
C.3x+2yЉ7=0Лђ4x+yЉ6=0
D.2x+3yЉ7=0Лђx+4yЉ6=0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМФГзлвеНкФПЯжГЁЩшгаAЃЌBЃЌCЃЌDЫФИіЙлжкЯЏЃЌЯжгагЩ5ВЛЭЌбеЩЋЕФТэМзПЩЙЉЯжГЁЙлжкбЁдёЃЌЭЌвЛЙлжкЯЏЩЯЕФТэМзЕФбеЩЋЯрЭЌЃЌЯрСкЙлжкЯЏЩЯЕФТэМзЕФбеЩЋВЛЯрЭЌЃЌдђВЛЭЌЕФАВХХЗНЗЈжжЪ§ЮЊ ЃЎ 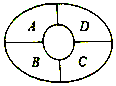
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() Чв
Чв![]() .
.
ЃЈ1ЃЉШєКЏЪ§![]() ЧјМф
ЧјМф![]() ЩЯЕЅЕїЕндіЃЌЧѓЪЕЪ§
ЩЯЕЅЕїЕндіЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЩшКЏЪ§![]() ЃЌ
ЃЌ ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§.ШєДцдк
ЮЊздШЛЖдЪ§ЕФЕзЪ§.ШєДцдк![]() ЃЌЪЙВЛЕШЪН
ЃЌЪЙВЛЕШЪН![]() ГЩСЂЃЌЧѓЪЕЪ§
ГЩСЂЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЕФзюаЁе§жмЦкЮЊ
ЕФзюаЁе§жмЦкЮЊ![]() .
.
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФЕЅЕїдіЧјМфЃЛ
ЕФЕЅЕїдіЧјМфЃЛ
ЃЈ2ЃЉНЋКЏЪ§![]() ЕФЭМЯѓЯђзѓЦНвЦ
ЕФЭМЯѓЯђзѓЦНвЦ![]() ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛЃЌЕУЕНКЏЪ§
ИіЕЅЮЛЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛЃЌЕУЕНКЏЪ§![]() ЕФЭМЯѓЃЌШє
ЕФЭМЯѓЃЌШє![]() дк
дк![]() ЩЯжСЩйКЌга10ИіСуЕуЃЌЧѓ
ЩЯжСЩйКЌга10ИіСуЕуЃЌЧѓ![]() ЕФзюаЁжЕ.
ЕФзюаЁжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖ![]() жаЃЌЕзУц
жаЃЌЕзУц![]() ЮЊЬнаЮЃЌ
ЮЊЬнаЮЃЌ ![]() ЕзУц
ЕзУц![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎЁЁ
ЃЎЁЁ

ЃЈ1ЃЉЧѓжЄЃКЦНУц![]()
![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩш![]() ЮЊ
ЮЊ![]() ЩЯЕФвЛЕуЃЌТњзу
ЩЯЕФвЛЕуЃЌТњзу![]() ЃЌШєжБЯп
ЃЌШєжБЯп![]() гыЦНУц
гыЦНУц![]() ЫљГЩНЧЕФе§ЧажЕЮЊ
ЫљГЩНЧЕФе§ЧажЕЮЊ![]() ЃЌЧѓЖўУцНЧ
ЃЌЧѓЖўУцНЧ![]() ЕФгрЯвжЕЃЎ
ЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com