
【题目】设函数![]() 有两个极值点
有两个极值点![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证:![]() .
.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,以
,以![]() 的短轴为直径的圆与直线
的短轴为直径的圆与直线![]() 相切.
相切.
(1)求![]() 的方程;
的方程;
(2)直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() .已知
.已知![]() 上存在点
上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰直角三角形,若
为顶角的等腰直角三角形,若![]() 在直线
在直线![]() 的右下方,求
的右下方,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是某景区的两条道路(宽度忽略不计,
是某景区的两条道路(宽度忽略不计,![]() 为东西方向),Q为景区内一景点,A为道路
为东西方向),Q为景区内一景点,A为道路![]() 上一游客休息区,已知
上一游客休息区,已知![]() ,
,![]() (百米),Q到直线
(百米),Q到直线![]() ,
,![]() 的距离分别为3(百米),
的距离分别为3(百米),![]() (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路
(百米),现新修一条自A经过Q的有轨观光直路并延伸至道路![]() 于点B,并在B处修建一游客休息区.
于点B,并在B处修建一游客休息区.
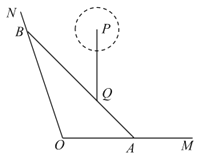
(1)求有轨观光直路![]() 的长;
的长;
(2)已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时,![]() (百米)(
(百米)(![]() ,
,![]() ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道
).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道![]() 以
以![]() (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
(百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,过右焦点
,过右焦点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.当
两点.当![]() 时,
时,![]() 是椭圆
是椭圆![]() 的下顶点,且
的下顶点,且![]() 的周长为6.
的周长为6.

(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆![]() 的右顶点为
的右顶点为![]() ,直线
,直线![]() 、
、![]() 分别与直线
分别与直线![]() 交于
交于![]() 、
、![]() 点,证明:当
点,证明:当![]() 变化时,以线段
变化时,以线段![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机厂商在销售200万台某型号手机时开展“手机碎屏险”活动、活动规则如下:用户购买该型号手机时可选购“手机碎屏险”,保费为![]() 元,若在购机后一年内发生碎屏可免费更换一次屏幕.该手机厂商将在这
元,若在购机后一年内发生碎屏可免费更换一次屏幕.该手机厂商将在这![]() 万台该型号手机全部销售完毕一年后,在购买碎屏险且购机后一年内未发生碎屏的用户中随机抽取
万台该型号手机全部销售完毕一年后,在购买碎屏险且购机后一年内未发生碎屏的用户中随机抽取![]() 名,每名用户赠送
名,每名用户赠送![]() 元的红包,为了合理确定保费
元的红包,为了合理确定保费![]() 的值,该手机厂商进行了问卷调查,统计后得到下表(其中
的值,该手机厂商进行了问卷调查,统计后得到下表(其中![]() 表示保费为
表示保费为![]() 元时愿意购买该“手机碎屏险”的用户比例);
元时愿意购买该“手机碎屏险”的用户比例);
(1)根据上面的数据求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)通过大数据分析,在使用该型号手机的用户中,购机后一年内发生碎屏的比例为![]() .已知更换一次该型号手机屏幕的费用为
.已知更换一次该型号手机屏幕的费用为![]() 元,若该手机厂商要求在这次活动中因销售该“手机碎屏险”产生的利润不少于
元,若该手机厂商要求在这次活动中因销售该“手机碎屏险”产生的利润不少于![]() 万元,能否把保费
万元,能否把保费![]() 定为5元?
定为5元?
x | 10 | 20 | 30 | 40 | 50 |
y | 0.79 | 0.59 | 0.38 | 0.23 | 0.01 |
参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为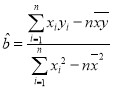 ,
,
![]() ,
,
参考数据:表中![]() 的5个值从左到右分别记为
的5个值从左到右分别记为![]() ,相应的
,相应的![]() 值分别记为
值分别记为![]() ,经计算有
,经计算有![]() ,其中
,其中![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左、右焦点,离心率为
的左、右焦点,离心率为![]() ,
,![]() 是平面内两点,满足
是平面内两点,满足![]() ,线段
,线段![]() 的中点
的中点![]() 在椭圆上,
在椭圆上,![]() 周长为12.
周长为12.
(1)求椭圆![]() 的方程;
的方程;
(2)若过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,求
,求![]() (其中
(其中![]() 为坐标原点)的取值范围.
为坐标原点)的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com